Question

Cho hình hộp ABCD.A’B’C’D’ (H.2.14).

a) Hai vectơ \(\overrightarrow {AB}  + \overrightarrow {AD} \) và \(\overrightarrow {AC} \) có bằng nhau hay không?

b) Hai vectơ \(\overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {AA'} \) và \(\overrightarrow {AC'} \) có bằng nhau hay không?

Answer 1

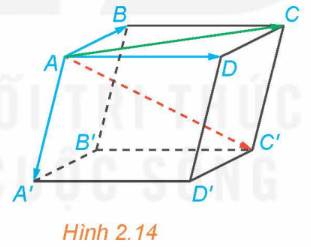
a) Vì ABCD là hình bình hành nên \(\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AC} \)

b) Ta có: \(\overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {AA'}  = \overrightarrow {AC}  + \overrightarrow {AA'} \) (1)

Vì ABCD. A’B’C’D’ là hình hộp nên AA’D’D và DD’C’C là hình bình hành. Do đó, AA’//DD’, \(AA' = DD'\) và \(DD' = CC'\), DD’//CC’. Suy ra, AA’//CC’ và \(AA' = CC'\). Suy ra, tứ giác AA’C’C là hình bình hành. Suy ra: \(\overrightarrow {AC}  + \overrightarrow {AA'}  = \overrightarrow {AC'} \) (2)

Từ (1) và (2) ta có: \(\overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {AA'}  = \overrightarrow {AC'} \)