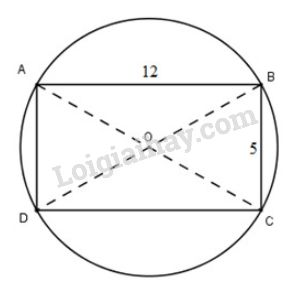
Gọi OO là giao điểm hai đường chéo của hình chữ nhật, ta có OA=OB=OC=OD=ROA=OB=OC=OD=R.
Suy ra bốn điểm A, B, C, DA, B, C, D cách đều điểm OO nên bốn điểm này cùng thuộc đường tròn tâm OO.
Xét tam giác ABCABC vuông tại BB, áp dụng định lí Pytago, ta có:
AC2=AB2+BC2=122+52=169AC2=AB2+BC2=122+52=169
⇒AC=√169=13.⇒AC=169=13.
Bán kính của đường tròn là: R=OB=OA=OC=OD=AC2=132=6,5.
Cho hình chữ nhật ABCD có AB = 12 cm, BC = 5cm. Chứng minh rằng bốn điểm A, B, C, D thuộc cùng một đường tròn. Tính bán kính của đường tròn đó ?
Cho hình chữ nhật ABCD có AD = 12 cn, CD = 16cm. Chứng minh rằng bốn điểm ABCD thuộc cùng một đường tròn. Tính bán kính của đường tròn đó ?
1. Cho tam giác ABC, góc A = 90 độ, có AB = 5 cm, AC = 12 cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
2. Cho hình thang cân ABCD (AD//BC). Biết AB = 12 cm, AC = 16 cm và BC = 20 cm. Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.
Bài 1: Cho hình chữ nhật ABCD.
a) Chứng minh rằng bốn điểm A, B, C và D cùng thuộc một đường tròn.
b) Cho AB = 10cm và BC = 6cm. Tính bán kính của đường tròn trên.
Cho hình thang cân ABCD (AD//BC). Biết AB=12cm, AC= 16cm và BC= 20cm. Chứng minh rằng 4 điểm A, B, C, D thuộc một đường tròn, tính bán kính của đường tròn đó
Cho hình chữ nhật ABCD. Biết AB=3cm, AD=4cm.Chứng minh 4 điểm ABCD cùng thuộc 1 đường tròn, tìm tâm, tính bán kính của đường tròn đó.
Cho hình vuông ABCD
a) Chứng minh rằng bốn đỉnh của hình vuông cùng nằm trên một đường tròn. Hãy chỉ ra vị trí của tâm đường tròn đó ?
b) Tính bán kính của đường tròn đó, biết cạnh của hình vuông bằng 2 dm ?
Bài 1.3: Cho hình vuông ABCD cạnh a.
a) Chứng minh: bốn đỉnh A, B, C và D của hình vuông trên cùng nằm trên một đường tròn.
b) Xác định tâm và bán kính của đường tròn đó.
Cho tứ giác ABCD có A = C = 90 độ . Chứng minh A , B , C , D cùng nằm trên một đường tròn . Xác định tâm và bán kính của đường tròn đó
