Question

Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn AB. Gọi M là trung điểm cạnh SA.

a) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD)

b) Xác định thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng (MCD). Tìm điều kiện của đáy ABCD để thiết diện là hình bình hành 

Answer 1

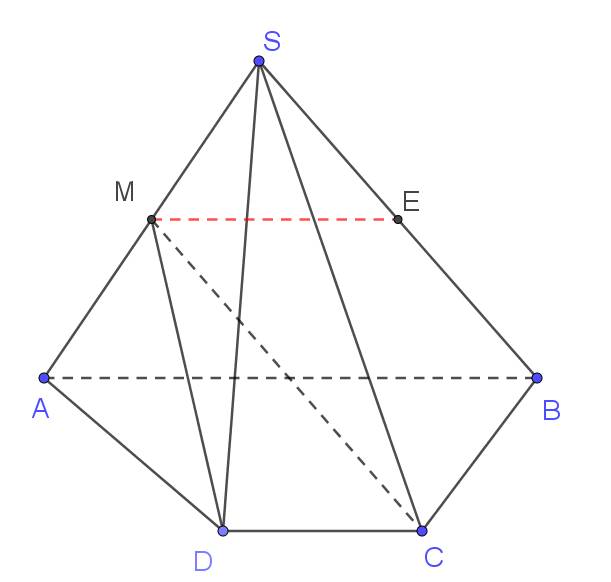
a) Điểm chung thứ nhất của hai mặt phẳng (SAB) và (SCD) là S.

Do AB // CD, do đó giao tuyến của hai mp đi qua S và song song với CD.

b) Dựng giao tuyến giữa (MCD) với (SAB).

Điểm chung thứ nhất là M.

Ta có CD // AB (CD \(\subset\) (MCD) ; AB \(\subset\) (SAB)), do đó giao tuyến của hai mp là đường thẳng đi qua M và song song với AB và CD. 

Đường thẳng này cắt SB tại E.

Ta chứng minh được ME//AB//DC và ME = AB : 2 (định lí đường trung bình trong tam giác).

Do đó để thiết diện MECD là hình bình hành thì ME = CD, tức là CD = AB / 2.