Vì SGKF=\(\dfrac{1}{2}.S_{GHF}\) (1)
SGFL= \(\dfrac{1}{2}.S_{GFT}\) (2)
Cộng (1) và (2) vế theo vế:
=> SGKL=\(\dfrac{1}{2}.\left(S_{GHF}+S_{GFT}\right)=\dfrac{1}{2}.S_{GTH}=\dfrac{1}{2}S\)
Nhớ tick nhé ,thank nhiều
Cho hình bs.30 (hình bình hành MNPQ có diện tích S và X, Y tương ứng là trung điểm của các cạnh QP, PN). Khi đó, diện tích của tứ giác MXPY bằng :
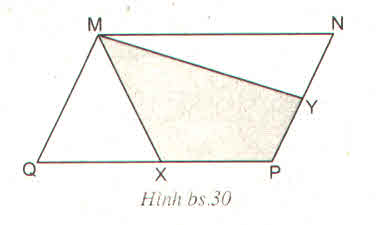
(A) \(\dfrac{1}{4}S\) (B) \(\dfrac{1}{2}S\)
(C) \(\dfrac{1}{8}S\) (D) \(\dfrac{3}{4}S\)
Chọn phương án đúng ?
Cho hình bs.31
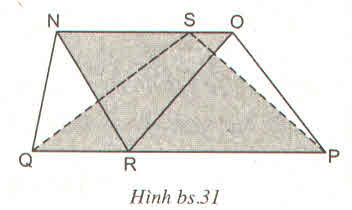
(R là điểm bất kì trên QP. S là điểm bất kì trên NO, hình thang NOPQ có diện tích S). Khi đó, tổng diện tích của hai tam giác QSP và NRO bằng :
(A) \(\dfrac{1}{2}S\) (B) \(\dfrac{1}{4}S\)
(C) \(\dfrac{3}{4}S\) (D) \(S\)
Hãy lựa chọn phương án đúng ?
Cho tứ giác MNPQ và các kích thước đã cho trên hình bs.28. Diện tích tam giác MQP bằng bao nhiêu \(cm^2\) ?
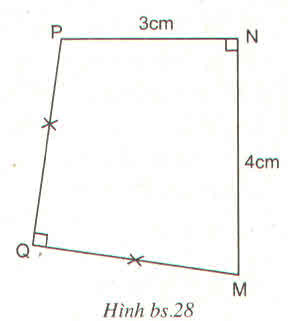
(A) 6 (B) 25
(C) \(\dfrac{25}{2}\) (D) \(\dfrac{25}{4}\)
Chọn phương án đúng ?
Cho tam giác MNP. Điểm T nằm trong tam giác MNP sao cho các tam giác TMN, TMP, TPN có diện tích bằng nhau. Khi đó, T là giao điểm
(A) ba đường cao của tam giác đó
(B) ba đường trung trực của tam giác đó
(C) ba đường trung tuyến của tam giác đó
(D) ba đường phân giác trong của tam giác đó
Hãy lựa chọn phương án đúng ?
Cho tam giác ABC. Gọi M, N là các trung điểm tương ứng của AC, BC. Chứng minh rằng diện tích của hình thang ABNM bằng \(\dfrac{3}{4}\) diện tích của tam giác ABC ?
1/ a. Chứng minh công thức Hê-rông tính diện tích tam giác theo 3 cạnh a,b,c S=\(\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\) (p là nửa chu vi)
b. Áp dụng chứng minh rằng nếu \(S=\dfrac{1}{4}\left(a+b-c\right)\left(a+c-b\right)\) thì tam giác đó là tam giác vuông
2/ Cho tứ giác ABCD. Lấy \(M,N\in AB\) sao cho AM=MN=NB. Lấy \(E,F\in BC\) sao cho BE=EF=FC. Lấy \(P,Q\in CD\) sao cho CP=PQ=QD. Lấy \(G,H\in AD\) sao cho DG=GH=HA. Gọi A',B' là giao điểm của MQ và NP với EH, C',D' là giao điểm của MQ và NP với FG. Chứng minh rằng
a. \(S_{MNPQ}=\dfrac{1}{3}S_{ABCD}\) b. \(S_{A'B'C'D'}=\dfrac{1}{9}S_{ABCD}\)
3/ Lấy M tùy ý nằm trong tam giác ABC. Gọi D,E,F là hình chiếu của M trên BC,AC,AB. Đặt BC=a,AC=b,AB=c,MD=x,ME=y,MF=z. Chứng minh rằng
a. ax+by+cz=2S (S=Sabc)
b. \(\dfrac{a}{x}+\dfrac{b}{y}+\dfrac{c}{z}\ge\dfrac{2p^2}{S}\) (\(p=\dfrac{a+b+c}{2}\) )
Cho hình bs.32 (tam giác MNP vuông tại đỉnh M và NRQP, PUTM, MKHN đều là hình vuông còn \(S_1,S_2,S_3\) tương ứng là diện tích của mỗi hình)
Q
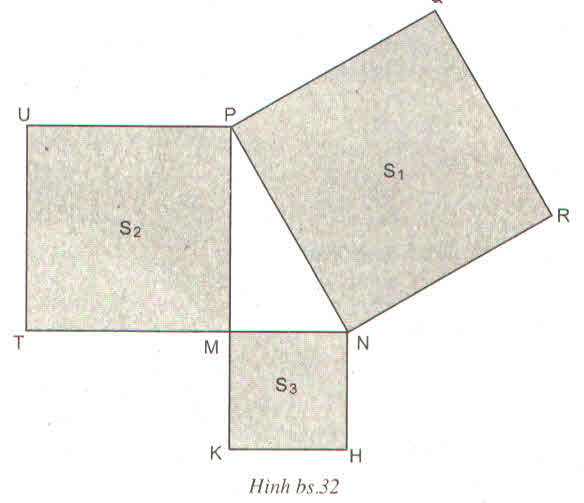
Quan hệ nào sau đây đúng ?
(A) \(S_3+S_2=S_1\) (B) \(S^2_3+S^2_2=S^2_1\)
(C) \(S_3+S_2>S_1\) (D) \(S^2_3+S^2_2< S^2_1\)
Hãy lựa chọn phương án đúng ?
Cho ΔABC có S = 60cm2, điểm D thuộc cạnh AB, điểm E thuộc cạnh AC sao cho AD = \(\dfrac{1}{3}\)AB, AE = \(\dfrac{1}{4}\)AC. Tính SDBEC
Mọi người giúp mình với ạ, mình đang cần gấp
Trên cạnh AB,AC của tam giác ABC lấy tương ứng 2 điểm M,N sao cho \(AM=\dfrac{1}{3}AB,AN=\dfrac{1}{3}AC\) . Gọi D là giao điểm của BN và CM. Qua A kẻ \(AH\perp BN,CK\perp BN\)
a) So sánh AH và CK
b) CM: \(S_{ABD}=\dfrac{1}{2}S_{BCD}\)
c) Biết \(S_{ABC}=24cm^2\)
Tính \(S_{AMDN}\)
