Bài 2: Diện tích hình chữ nhật
Các câu hỏi tương tự
Cho hình bình hành ABCD. Đường phân giác của các góc A và C cắt đường chéo BD tại E và F

a) Chứng minh rằng hai hình ABCFE và ADCFE có cùng diện tích
b) Các hình đó có phải là đa giác lồi không ? Vì sao ?
Cho hình chữ nhật ABCD với AB = 8cm, đường chéo BD = 10cm. Gọi H là chân đường góc kẻ từ A đến BD. Gọi M và N lần lượt là trung điểm của các đoạn AH và DH.
a) Chứng minh rằng MN//AD
b) Tính diện tích ABCD
Giúp mình mai mình thi rồi
Trên hình dưới đây, các tứ giác ABCD và EFCH đều là hình bình hành. Điểm E nằm trên đường chéo AC

a) Chứng minh rằng đa giác AEHD và hình ABCFE có cùng diện tích
b) ABCFE có phải là đa giác lồi không ? Vì sao ?
Cho tứ giác ABCD gọi M N P Q lần lượt là trung điểm của các cạnh AB BC CD DA
A) Chứng minh tứ giác MNPQ là hình bình hành
b) tìm điều kiện hai đường chéo AC và BD của tứ giác ABCD để MNPQ là hình chữ nhật
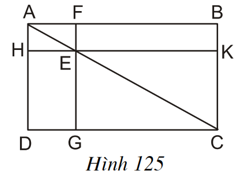
Cho hình 125, trong đó ABCD là hình chữ nhật, E là một điểm bất kì nằm trên đường chéo AC, FG // AD và HK // AB. Chứng minh rằng hai hình chữ nhật EFBK và EGDH có cùng diện tích.
Đọc tiếp
Cho hình 125, trong đó ABCD là hình chữ nhật, E là một điểm bất kì nằm trên đường chéo AC, FG // AD và HK // AB. Chứng minh rằng hai hình chữ nhật EFBK và EGDH có cùng diện tích.
Cho tam giác ABC vuông tại A (AB AC) có trung tuyến AM. Kẻ MN vuông góc AB và MP vuông góc AC (N thuộc AB, P thuộc AC).a. Tứ giác ANMP là hình gì? Vì sao?b. Chứng minh: NA NB, PA PC và tứ giác BMPN là hình bình hành.
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC) có trung tuyến AM. Kẻ MN vuông góc AB và MP vuông góc AC (N thuộc AB, P thuộc AC).
a. Tứ giác ANMP là hình gì? Vì sao?
b. Chứng minh: NA = NB, PA = PC và tứ giác BMPN là hình bình hành.
Cho hình 125:
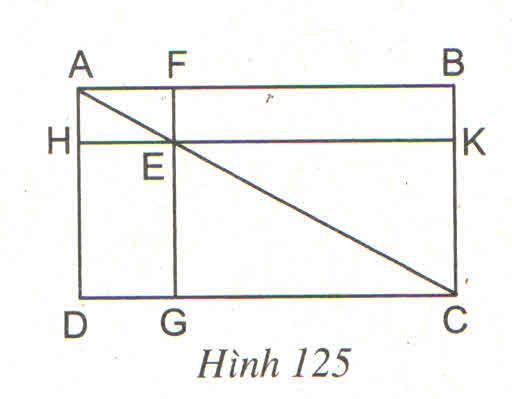
Trong đó ABCD là hình chữ nhật, E là một điểm bất kì nằm trên đường chéo AC, FG // AD và HK // AB
Chứng minh rằng hai hình chữ nhật EFBK và EGDH có cùng diện tích ?
Cho tam giác ABC vuông tại A (AB AC) có trung tuyến AM. Kẻ MN vuông góc AB và MP vuông góc AC (N thuộc AB, P thuộc AC).a. Tứ giác ANMP là hình gì? Vì sao? b. Chứng minh: NA NB, PA PC và tứ giác BMPN là hình bình hành.c.Gọi E là trung điểm BM; F là giao điểm của AM và PN. Chứng minh: - Tứ giác ABEF là hình thang cân; - Tứ giác MENF là hình thoi. d. Kẻ đường cao AH của tam giác ABC, MK // AH (K thuộc AC). Chứng minh: BK vuô...
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC) có trung tuyến AM. Kẻ MN vuông góc AB và MP vuông góc AC (N thuộc AB, P thuộc AC).
a. Tứ giác ANMP là hình gì? Vì sao?
b. Chứng minh: NA = NB, PA = PC và tứ giác BMPN là hình bình hành.
c.Gọi E là trung điểm BM; F là giao điểm của AM và PN. Chứng minh:
- Tứ giác ABEF là hình thang cân;
- Tứ giác MENF là hình thoi.
d. Kẻ đường cao AH của tam giác ABC, MK // AH (K thuộc AC). Chứng minh: BK vuông góc HN.
Cho một tam giác vuông cân. Chứng minh rằng tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông bằng diện tích của hình vuông dựng trên cạnh huyền (không sử dụng định lí Py-ta-go) ?