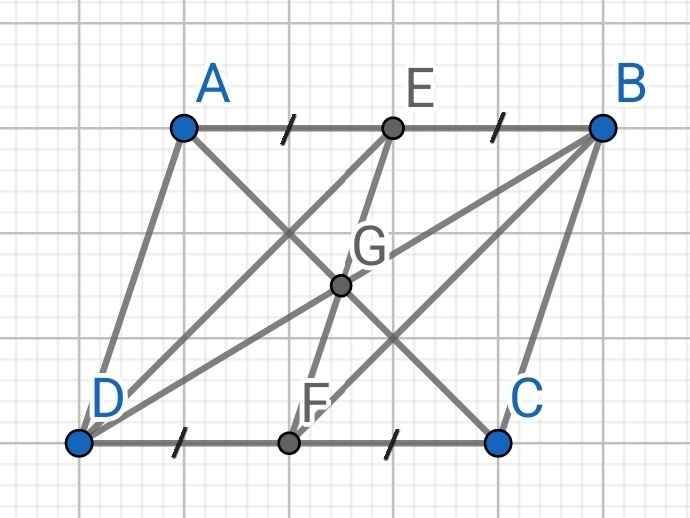
 a) Do ABCD là hình bình hành (gt)
a) Do ABCD là hình bình hành (gt)
⇒ AB // CD
⇒ BE // DF
Do ABCD là hình bình hành
⇒ AB = CD (1)
Ta có:
E là trung điểm của AB (gt)
⇒ BE = AB : 2 (2)
F là trung điểm của CD (gt)
⇒ DF = CD : 2 (3)
Từ (1), (2) và (3) ⇒ BE = DF
Tứ giác BFDE có:
BE // DF (cmt)
BE = DF (cmt)
⇒ BFDE là hình bình hành
b) Gọi G là trung điểm của AC
Do ABCD là hình bình hành (gt)
⇒ G là trung điểm của AC và BD (4)
Do BFDE là hình bình hành (cmt)
G là trung điểm của BD (cmt)
⇒ G là trung điểm của EF (5)
Từ (4) và (5) ⇒ AC, BD, EF cắt nhau tại G










