Đầu bài vô lí qua CK kẻ đg thg vuông BD tại F , cắt AC tại K
CK nào???
1: Xét ΔAED vuông tại E và ΔCFB vuông tại F có
AD=CB
\(\widehat{ADE}=\widehat{CBF}\)
Do đó: ΔAED=ΔCFB
Suy ra: AE=CF
Ta có: AE\(\perp\)BD
CF\(\perp\)BD
Do đó: AE//CF
Đầu bài vô lí qua CK kẻ đg thg vuông BD tại F , cắt AC tại K
CK nào???
1: Xét ΔAED vuông tại E và ΔCFB vuông tại F có
AD=CB
\(\widehat{ADE}=\widehat{CBF}\)
Do đó: ΔAED=ΔCFB
Suy ra: AE=CF
Ta có: AE\(\perp\)BD
CF\(\perp\)BD
Do đó: AE//CF
Cho hình bình hành ABCD có AB > AD . qua A kẻ đg thg vuông BD tại E , cắt CD tại I . qua C kẻ đg thg vuông BD tại F , cắt AC tại K
1) Chứng minh : AE // CF và AE = CF
2) Tứ giác AECI là hình gì ? Vì sao ?
Cho hình bình hành ABCD có AB > AD . qua A kẻ đg thg vuông BD tại E , cắt CD tại I . qua CK kẻ đg thg vuông BD tại F , cắt AC tại K.
a, CM : tứ giác AECI là hình gì vì sao
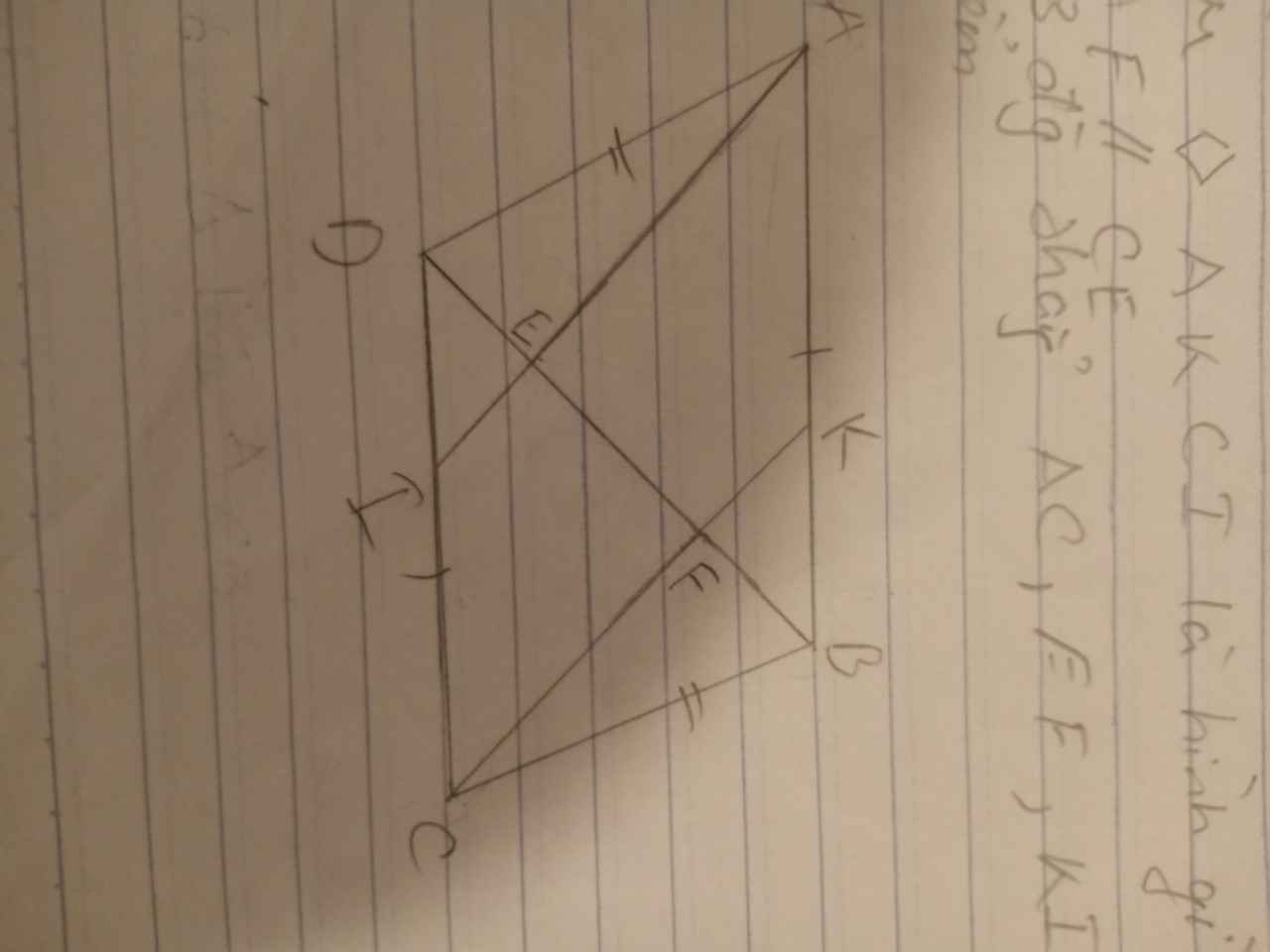
Cho hình bình hành ABCD (AB>AD). Qua A kẻ đường thẳng vuông góc với BD tại E, cắt CD tại I. Qua C, kẻ đường thẳng vuông góc với BD tại F cắt AB tại K.
a) Tứ giác AKCI là hình gì? Vì sao?
b) CM: AF//CE
c) CM: AC, EF, KI đồng quy
Cho hình bình hành ABCD, E, F thuộc đường chéo BD, sao cho BE = DF
a/ Chứng minh AE // CF
b/ AE cắt BC tại K, CF cắt AD tại I. Chứng minh tứ giác AKCI là hình bình hành
Cho hình bình hành ABCD, Có hai đường chéo AC và BD cắt nhau tại O. Từ A kẻ AE vuông góc với BD, từ C kẻ CF vuông góc với BD. Chứng minh rằng Tứ giác AECF là hình bình hành.
Cho hình bình hành ABCD có đường chéo BD tại M , cắt CD tại E . Từ C kẻ đường thẳng vuông góc BD tại N , cắt AB tại F. Chứng minh rằng : a) tam giác AMD = tam giác CNB b) tứ giác AMCN là hình bình hành c) tứ giác AECF là hình bình hành ( CÓ HÌNH VẼ) GIÚP EM VỚI Ạ EM ĐANG CẦN GẤP
Bài 4: Cho hình bình hành ABCD, hai đường chéo AC, BD cắt nhau tại O. Kẻ BH I AC tại H cắt DC tại N và kẻ DK 1 AC tại K cắt AB tại M. a) Chứng minh tứ giác BMDN là hình bình hành. b) Chứng minh tứ giác BKDH là hình bình hành. c) Chứng minh AC, BD, MN đồng quy.
Cho hình bình hành ABCD,hai đường chéo AC,BD cắt nhau tại O.Kẻ BH vuông góc AC tại H,cắt DC tại N và kẻ DK vuông góc AC tại K cắt AB tại M.CMR:
a,Tứ giác BMDN là hình bình hành ;
b,Tứ giác BKDH là hình bình hành;
c,AC,BD,MN đồng quy
Cho hình bình hành ABCD có góc A từ và AB>BC.Kẻ AH vuông góc với DC tại H,CK vuông góc với AB tại K.a,Tứ giác AKCH là hình gì? b,Gọi E là giao điểm của BD và AH,F là giao điểm của BD và CK.Chứng minh rằng HDE=KBF và AF=CE c,AF cắt BC tại I và CE cắt AD tại J.Chứng minh IJ,HK,BD cùng đi qua 1 điểm