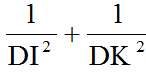Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
Các câu hỏi tương tự
Cho tam giác nhọn ABC có đường cao AH và đường trung tuyến AM. Biết góc B = 57độ ,AB =9cm, AC = 12cm.Giải tam giác ABC và tính AM
Giúp mk với nhé cảm ơn nhiều mk sẽ tick cho
Cho tam giác ABC (AB<AC) có góc A bằng 90* và M là trung tuyến của B. Gọi H là hình chiếu của A trên BC. Cho biết AM=13cm; AH=12cm
a) tính MH; AB; AC
b) Đường thẳng qua B và vuông góc với AM cắt AC tại F. Tính AF;BF
cho △ABC⊥A, đường cao AH, D và E lần lượt là hình chiếu của H trên AB, AC. chứng minh
a)\(\dfrac{HB}{HC}=\left(\dfrac{AB}{AC}\right)^2\)
b)\(\dfrac{CE}{BD}=\left(\dfrac{CA}{AB}\right)^3\)
c)\(AH^3=BC.BD.CE\)
d)\(3AH^2+BD^2+CE^2=BC^2\)
lm nhanh giúp mk nhé! Mk đang càn gấp lắm!
Cho tam giác ABC, góc A =90°, AH vuông góc với BC( H€BC) , BH=4 cm, CH= 9cm. a, Tính AB(chính xác đến0,01) và diện tích∆ABC b, tính góc B(chính xác đến phút) c, kẻ HM vuông góc với AB, HN vuông góc với AC (M € AB, N€ AC). CMR AH^3 = BC.BM.CN
cho tam giác ABC (góc A =90độ)AH vuông góc với BC biết AB/AC=3/4 AH=9cm tính AB AC BC BH CH
Hãy sắp xếp các tỉ số lượng giác theo thứ tự Giảm dần ( không dùng bảng và máy tính)
a) tan42 độ ,tan56 độ, cot3 độ, cot18 độ.
b) sin13 độ, cos47 độ, tan46 độ, cot2 độ.
Giúp mk với nhé. Mong các bạn giải các bước hộ mk. CẢM ƠN! Mk hứa sẽ tick cho.
giúp mk bài này vs Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng:a) Tam giác DIL là một tam giác cânb) Tổngkhông đổi khi I thay đổi trên cạnh AB.
Đọc tiếp
giúp mk bài này vs
Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng:
a) Tam giác DIL là một tam giác cân
b) Tổng
không đổi khi I thay đổi trên cạnh AB.
Cho góc xOy=90°. Trên tia Ox lấy điểm A, tia Ax lấy điểm N, Oy lấy điểm M sao cho AN=OM. Nối M vs N. I là trung điểm của MN. CMR I di chuyển trên một đường thẳng cố định.
Giúp mk với mk ko biết nó thuộc phần nào ak. Mk cảm ơn nhiều.
cho tam giác ABC vuông tại A, đường cao AH . Cho biết BH =4, CH=9cm. Gọi D,E lần lượt là hình chiếu vuông góc của H trên cạnh AB, AC. Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M,N. Tính diện tích tứ giác DENM
MÌNH ĐANG CẦN GẤP MN GIÚP MIK VS Ạ ! MIK CẢM ƠN !