Ta có: \(f'\left(x\right)=2x-2\Rightarrow f'\left(-1\right)=2\cdot\left(-1\right)-2=-4\)
Phương trình tiếp tuyến với (C) tại điểm M là:
\(y=f'\left(x_0\right)\left(x-x_0\right)+f\left(x_0\right)=-4\left(x+1\right)+6=-4x+2\)
Ta có: \(f'\left(x\right)=2x-2\Rightarrow f'\left(-1\right)=2\cdot\left(-1\right)-2=-4\)
Phương trình tiếp tuyến với (C) tại điểm M là:
\(y=f'\left(x_0\right)\left(x-x_0\right)+f\left(x_0\right)=-4\left(x+1\right)+6=-4x+2\)
Cho hàm số \(y = {x^3} - 3{{\rm{x}}^2}\). Tiếp tuyến với đồ thị của hàm số tại điểm \(M\left( { - 1;4} \right)\) có hệ số góc bằng:
A. ‒3.
B. 9.
C. ‒9.
D. 72.
Cho hai hàm số \(f\left( x \right) = 2{{\rm{x}}^3} - {x^2} + 3\) và \(g\left( x \right) = {x^3} + \frac{{{x^2}}}{2} - 5\). Bất phương trình \(f'\left( x \right) > g'\left( x \right)\) có tập nghiệm là
A. \(\left( { - \infty ;0} \right] \cup \left[ {1; + \infty } \right)\).
B. \(\left( {0;1} \right)\).
C. \(\left[ {0;1} \right]\).
D. \(\left( { - \infty ;0} \right) \cup \left( {1; + \infty } \right)\).
Hàm số \(y = \frac{1}{{x + 1}}\) có đạo hàm cấp hai tại \(x = 1\) là
A. \(y''\left( 1 \right) = \frac{1}{2}\).
B. \(y''\left( 1 \right) = - \frac{1}{4}\).
C. \(y''\left( 1 \right) = 4\).
D. \(y''\left( 1 \right) = \frac{1}{4}\).
Hàm số \(y = \frac{{x + 3}}{{x + 2}}\) có đạo hàm là
A. \(y' = \frac{1}{{{{\left( {x + 2} \right)}^2}}}\).
B. \(y' = \frac{5}{{{{\left( {x + 2} \right)}^2}}}\).
C. \(y' = \frac{{ - 1}}{{{{\left( {x + 2} \right)}^2}}}\).
D. \(y' = \frac{{ - 5}}{{{{\left( {x + 2} \right)}^2}}}\).
Tinh đạo hàm của các hàm số sau:
a) \(y = \tan \left( {{e^x} + 1} \right)\);
b) \(y = \sqrt {\sin 3x} \);
c) \(y = \cot \left( {1 - {2^x}} \right)\).
Tính đạo hàm của các hàm số sau:
a) \(y = 3{x^4} - 7{x^3} + 3{x^2} + 1\);
b) \(y = {\left( {{x^2} - x} \right)^3}\);
c) \(y = \frac{{4{\rm{x}} - 1}}{{2{\rm{x}} + 1}}\)
Tính đạo hàm của các hàm số sau:
a) \(y = \left( {{x^2} + 3x - 1} \right){e^x}\);
b) \(y = {x^3}{\log _2}x\).
Nhiệt độ cơ thể của một người trong thời gian bị bệnh được cho bởi công thức \(T\left( t \right) = - 0,1{t^2} + 1,2t + 98,6\), trong đó \(T\) là nhiệt độ (tính theo đơn vị đo nhiệt độ Fahrenheit) tại thời điểm \(t\) (tính theo ngày). Tìm tốc độ thay đổi của nhiệt độ ở thời điểm \(t = 1,5\).
(Nguồn: https://www.algebra.com/algebra/homework/Trigonometry-basics/Trigonometry-basics.faq.question.1111985.html)
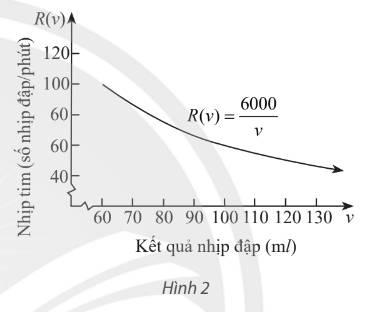
Hàm số \(R\left( v \right) = \frac{{6000}}{v}\) có thể được sử dụng để xác định nhịp tim \(R\) của một người mà tim của người đó có thể đây đi được \(6000ml\) máu trên mỗi phút và \(v{\rm{ }}ml\) máu trên mỗi nhịp đập (theo Bách khoa toàn thư Y học “Harrison's internal medicine 21st edition”). Tìm tốc độ thay đổi của nhịp tim khi lượng máu tim đẩy đi ở một nhịp là \(v = 80\).