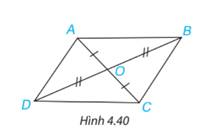
a) Xét \(\Delta AOB\) và \(\Delta COD\), có:
AO = CO (gt)
\(\widehat{AOB}=\widehat{COD}\) ( đối đỉnh)
OB = OD (gt)
\(\Rightarrow \Delta AOB = \Delta COD\) ( c.g.c)
Xét \(\Delta AOD\) và \(\Delta COB\), có:
AO = CO (gt)
\(\widehat{AOD}=\widehat{COB}\) ( đối đỉnh)
OD = OB (gt)
\(\Rightarrow \Delta AOD = \Delta COB\) ( c.g.c)
Vậy hai cặp tam giác có chung đỉnh O bằng nhau là: AOB và COD; AOD và COB theo trường hợp cạnh – góc – cạnh.
b)
Do \(\Delta AOD = \Delta COB\) nên: \(\widehat {ADO} = \widehat {CBO}\) (2 góc tương ứng) và AD=BC (2 cạnh tương ứng)
Xét \(\Delta DAB\) và \(\Delta BCD\), có:
AD=BC (cmt)
\(\widehat {ADO} = \widehat {CBO}\) (cmt)
BD chung
Vậy \(\Delta DAB =\Delta BCD\) (c.g.c)