+ Với mọi n ∈ N*, ta có:
|un – 2| ≤ vn ⇔ -vn ≤ un – 2 ≤ vn
+ Mà lim (-vn) = lim (vn) = 0 nên
lim (un – 2) = 0 ⇔ lim un – lim 2 = 0 ⇔ lim un = 2
Đúng 0
Bình luận (0)
Bài 4: Ôn tập chương Giới hạn
Các câu hỏi tương tự
Cho dãy số \(\left(u_n\right)\) xác định bởi \(\left\{{}\begin{matrix}u_1=1\\u_{n+1}=\dfrac{2u_n+3}{u_n+2},\left(n\ge1\right)\end{matrix}\right.\)
a) Chứng minh rằng \(u_n>0\) với mọi \(n\)
b) Biết \(\left(u_n\right)\) có giới hạn hữu hạn. Tìm giới hạn đó ?
Cho dãy số \(\left(u_n\right)\) thỏa mãn \(u_n< M\) với mọi \(n\). Chứng minh rằng nếu \(\lim\limits u_n=a\) thì \(a\le M\) ?
Tìm giới hạn của dãy số \(\left(u_n\right)\) với :
a) \(u_n=\dfrac{\left(-1\right)^n}{n^2+1}\)
b) \(u_n=\dfrac{2^n-n}{3^n+1}\)
Tính giới hạn của dãy số:
\(u_n=\dfrac{1}{2\sqrt{1}+\sqrt{2}}+\dfrac{1}{3\sqrt{2}+2\sqrt{3}}+...+\dfrac{1}{\left(n+1\right)\sqrt{n}+n\sqrt{n+1}}\)
Cho dãy số (Un) thỏa mãn \(\left|U_n-2\right|\le\frac{2018}{n^2},\forall n\ge1\)
Tính limUn ?
Tính giới hạn sau:
\(\lim\limits\sqrt{2\sqrt{2\sqrt{2...\sqrt{2}}}}\left(\text{n dấu căn}\right)\)
Tính các giới hạn sau (\(n\rightarrow+\infty\) )
a) \(\lim\limits\dfrac{\left(-3\right)^n+2.5^n}{1-5^n}\)
b) \(\lim\limits\dfrac{1+2+3+....+n}{n^2+n+1}\)
c) \(\lim\limits\left(\sqrt{n^2+2n+1}-\sqrt{n^2+n-1}\right)\)
Cho hai hàm số fleft(xright)dfrac{1-x^2}{x^2} và gleft(xright)dfrac{x^3+x^2+1}{x^2}
a) Tính limlimits_{xrightarrow0}fleft(xright);limlimits_{xrightarrow0}gleft(xright);limlimits_{xrightarrow+infty}fleft(xright);limlimits_{xrightarrow+infty}gleft(xright)
b) Hai đường cong sau đây (h.60) là đồ thị của hai hàm số đã cho. Từ kết quả câu a), hãy xác định xem đường con nào là đồ thị của mỗi hàm số đó ?
Đọc tiếp
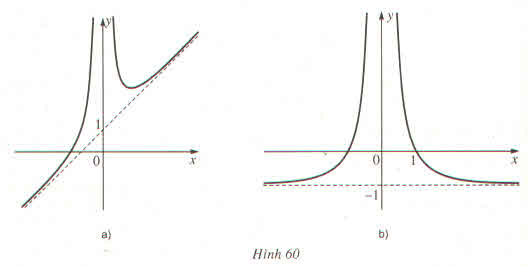
Cho hai hàm số \(f\left(x\right)=\dfrac{1-x^2}{x^2}\) và \(g\left(x\right)=\dfrac{x^3+x^2+1}{x^2}\)
a) Tính \(\lim\limits_{x\rightarrow0}f\left(x\right);\lim\limits_{x\rightarrow0}g\left(x\right);\lim\limits_{x\rightarrow+\infty}f\left(x\right);\lim\limits_{x\rightarrow+\infty}g\left(x\right)\)
b) Hai đường cong sau đây (h.60) là đồ thị của hai hàm số đã cho. Từ kết quả câu a), hãy xác định xem đường con nào là đồ thị của mỗi hàm số đó ?
Trong các giới hạn sau , giới hạn nào không tồn tại ?
A. \(lim\frac{x+1}{\sqrt{x-2}}\left(x\rightarrow1\right)\)
B. \(lim\frac{x+1}{\sqrt{-x+2}}\left(x\rightarrow-1\right)\)
C. \(lim\frac{x+1}{\sqrt{2-x}}\left(x\rightarrow1\right)\)
D. \(lim\frac{x+1}{\sqrt{2+x}}\left(x\rightarrow-1\right)\)