Cho hai đa thức:
\(P(x) = 4{x^2} + 1 + 3x\) và \(Q(x) = 5x + 2{x^2} + 3\).
a) Sắp xếp các đa thức P(x), Q(x) theo số mũ giảm dần của biến.
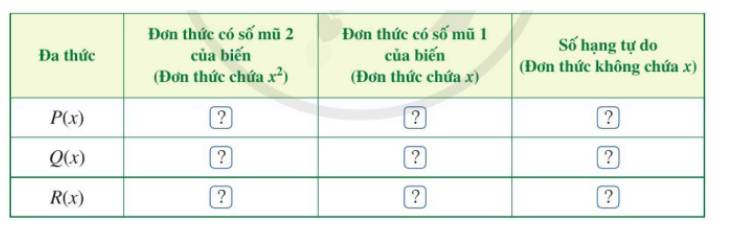
b) Tìm đơn thức thích hợp trong dạng thu gọn của P(x) và Q(x) cho ? ở bảng sau rồi trừ hai đơn thức theo từng cột và thể hiện kết quả ở dòng cuối cùng của mỗi cột:
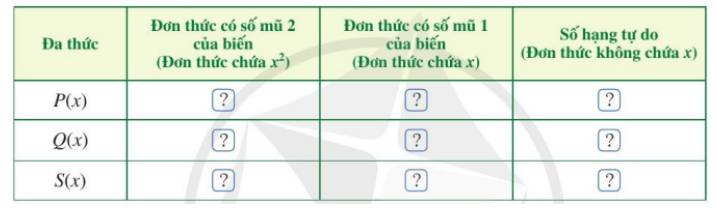
c) Dựa vào kết quả trừ hai đơn thức theo từng cột, xác định đơn thức S(x).
a) \(P(x) = 4{x^2} + 1 + 3x = 4{x^2} + 3x + 1\) ; \(Q(x) = 5x + 2{x^2} + 3 = 2{x^2} + 5x + 3\).
b)
Đa thức | Đơn thức có số mũ 2 của biến (Đơn thức chứa \({x^2}\)) | Đơn thức có số mũ 1 của biến (Đơn thức chứa x) | Số hạng tự do (Đơn thức không chứa x) |
P(x) | \(4{x^2}\) | 3x | 1 |
Q(x) | \(2{x^2}\) | 5x | 3 |
S(x) | \(2{x^2}\) | – 2x | – 2 |
c) Vậy \(S(x) = 2{x^2} - 2x - 2\)