Question

Cho hai đa thức: \(R(x) =  - 8{x^4} + 6{x^3} + 2{x^2} - 5x + 1\) và \(S(x) = {x^4} - 8{x^3} + 2x + 3\). Tính:

a) R(x) + S(x);                                                 b) R(x) – S(x).

Answer 1

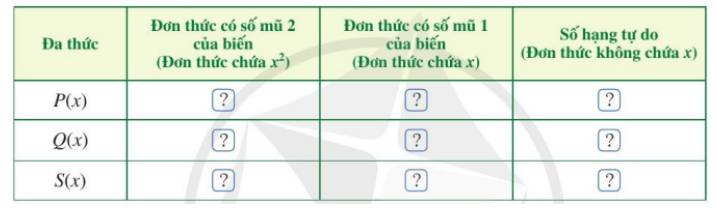
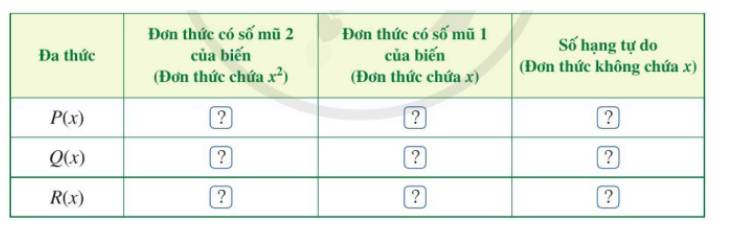
a)

\(\begin{array}{l}R(x) + S(x) =  - 8{x^4} + 6{x^3} + 2{x^2} - 5x + 1 + {x^4} - 8{x^3} + 2x + 3\\ = ( - 8 + 1){x^4} + (6 - 8){x^3} + 2{x^2} + ( - 5 + 2)x + (1 + 3)\\ =  - 7{x^4} - 2{x^3} + 2x - 3x + 4\end{array}\)

b)

\(\begin{array}{l}R(x) - S(x) =  - 8{x^4} + 6{x^3} + 2{x^2} - 5x + 1 - ({x^4} - 8{x^3} + 2x + 3)\\ =  - 8{x^4} + 6{x^3} + 2{x^2} - 5x + 1 - {x^4} + 8{x^3} - 2x - 3\\ = ( - 8 - 1){x^4} + (6 + 8){x^3} + 2{x^2} + ( - 5 - 2)x + (1 - 3)\\ =  - 9{x^4} + 14{x^3} + 2x - 7x - 2\end{array}\)