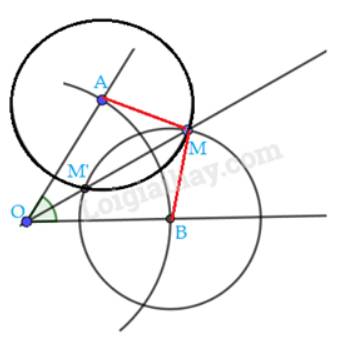
Ta có: AM = bán kính đường tròn tâm A
BM = bán kính đường tròn tâm B
Mà 2 đường tròn này có bán kính bằng nhau
Do đó, AM = BM
Xét \(\Delta \)OAM và \(\Delta \)OBM có:
OA = OB( = bán kính đường tròn tâm O)
MA = MB (cmt)
OM chung
\( \Rightarrow \) \(\Delta \)OAM = \(\Delta \)OBM ( c.c.c)
\( \Rightarrow \) \(\widehat {AOM} = \widehat {BOM}\) ( 2 góc tương ứng)
Mà OM nằm giữa 2 tia OA và OB
\( \Rightarrow \) OM là tia phân giác của góc AOB.