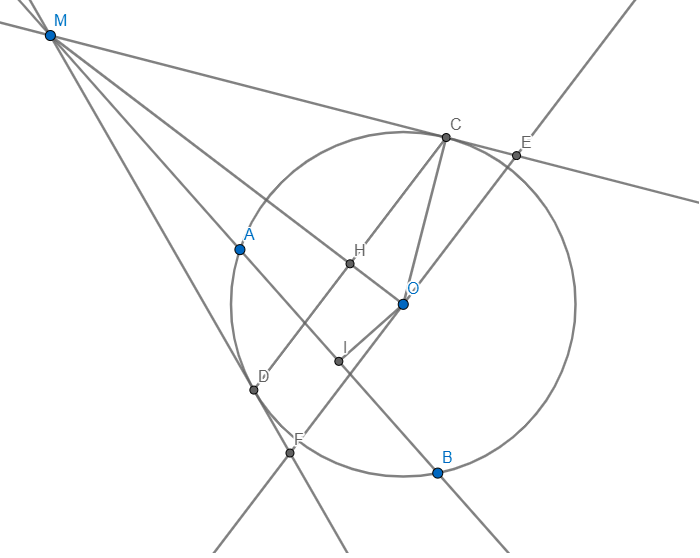
Cho đường tròn tâm O bán kính R. Một đường thẳng d không đi qua O và cắt đường tròn tại hai điểm
phân biệt A và B. Trên d lấy điểm M sao cho A nằm giữa M và B. Từ M kẻ hai tiếp tuyến MC và MD với
đường tròn (C, D là các tiếp điểm; các tia MA và MD nằm trên cùng nửa mặt phẳng bờ chứa tia MO). Gọi I là
trung điểm của AB. H là giao điểm của OM và CD.
a) Chứng minh rằng MIOC là tứ giác nội tiếp.
b) Một đường thẳng đi qua O và song song với CD cắt các tia MC và MD lần lượt tại E và F. Chứng
minh CM.CE = OH.OM . Xác định vị trí của M trên d sao cho diện tích tam giác MEF đạt giá trị nhỏ nhất.
Ai giải giúp với
a) Trong (O) có AB là dây cung không đi qua O và I là trung điểm AB
\(\Rightarrow OI\bot AB\Rightarrow\angle MIO=90\Rightarrow\angle MIO+\angle MCO=90+90=180\)
\(\Rightarrow MIOC\) nội tiếp
b) Vì MC,MD là tiếp tuyến \(\Rightarrow\Delta MCD\) cân tại M có MO là phân giác \(\angle CMD\) \(\Rightarrow MO\bot CD\) mà \(EF\parallel CD\) \(\Rightarrow EF\bot MO\)
tam giác MOE vuông tại O có đường cao OC \(\Rightarrow CM.CE=OC^2\)
tam giác MOC vuông tại C có đường cao HC \(\Rightarrow OH.OM=OC^2\)
\(\Rightarrow OH.OM=CM.CE\)
Vì H là trung điểm CD (\(\Delta MCD\) cân tại M) và \(EF\parallel CD\)
\(\Rightarrow O\) là trung điểm EF
\(\Rightarrow S_{MEF}=2S_{MOE}=2.\dfrac{1}{2}.OC.ME=OC.\left(CM+CE\right)\)
\(\ge R.\sqrt{CM.CE}=R.2\sqrt{OC^2}=R.2OC=2R^2\)
\(\Rightarrow S_{MEF_{min}}=2R^2\) khi \(CM=CE=R\left(CM.CE=R^2\right)\)
\(\Rightarrow OM=\sqrt{R^2+R^2}=\sqrt{2}R\)
Vậy M nằm trên d sao cho \(OM=\sqrt{2}R\) thì diện tích tam giác MEF nhỏ nhất \(\left(=2R^2\right)\)