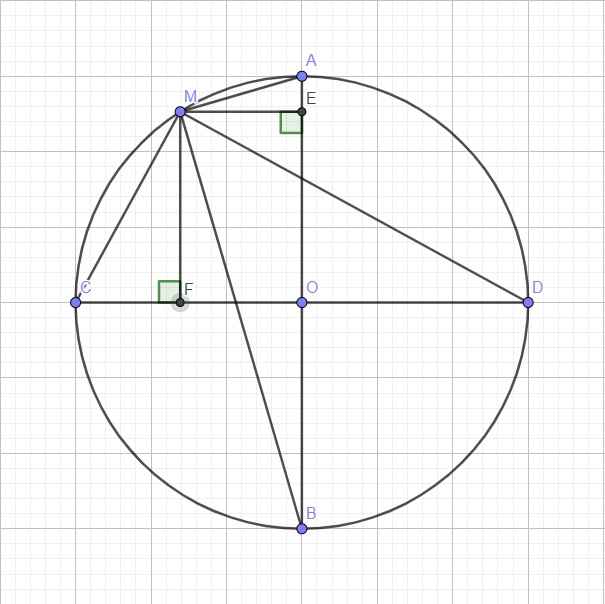
Do tính đối xứng, không mất tính tổng quát, giả sử M nằm trên cung nhỏ AC
Từ M lần lượt kẻ ME vuông góc AB và MF vuông góc CD
Do \(\widehat{AMB}\) là góc nội tiếp chắn nửa đường tròn \(\Rightarrow\widehat{AMB}=90^0\) hay tam giác AMB vuông tại M
Áp dụng hệ thức lượng: \(ME.AB=MA.MB\) \(\Leftrightarrow MA.MB=2R.ME\)
Tương tự: \(MC.MD=2R.MF\)
\(\Rightarrow MA.MB.MC.MD=4R^2.ME.MF\)
\(\Rightarrow\) Tích số đã cho đạt max khi \(ME.MF\) đạt max
Lại có tứ giác MEOF là hình chữ nhật (4 góc vuông)
\(\Rightarrow EF=MO=R\)
Áp dụng BĐT \(ab\le\dfrac{1}{2}\left(a^2+b^2\right)\) ta có:
\(ME.MF\le\dfrac{1}{2}\left(ME^2+MF^2\right)=\dfrac{1}{2}EF^2=\dfrac{1}{2}R^2\)
Dấu "=" xảy ra khi và chỉ khi \(ME=MF\) hay M nằm chính giữa cung AC
Vậy MA.MB.MC.MD đạt max khi M nằm chính giữa một trong các cung nhỏ AC, CB, BD hoặc DA