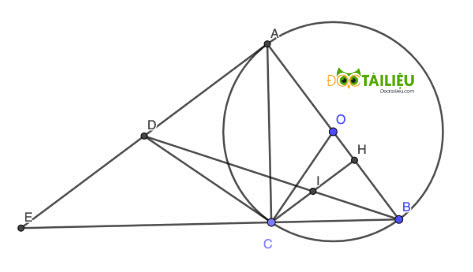
Cho đường tròn (O) và điểm A nằm trên đường tròn. Gọi d là tiếp tuyến của (O) tại A. Trên d lấy điểm D (D không trùng với A), kẻ tiếp tuyến DB của (O) (B là tiếp điểm, B không trùng với A)
a)CMR: Tứ giác AOBD nội tiếp
b) Trên tia đối của tia BA lấy điểm C. Kẻ DH vuông góc với OC( H thuộc OC). Gọi I là giao điểm của AB và OD. CMR: OH.OC=OI.OD
c) Gọi M là giao điểm của DH với cung nhỏ AB của (O). CMR: CM là tiếp tuyến của (O)
d) Gọi E là giao điểm của DH và CI. Gọi F là giao điểm thứ hai của đường tròn đường kính OD và đường tròn ngoại tiếp tam giác OIM. CMR: O,E,F thẳng hàng
a: góc OAD+góc OBD=180 độ
=>OADB nội tiếp
b: Xét (O) có
DA,DB là tiếp tuyến
=>DA=DB
mà OA=OB
nên OD là trung trực của AB
=>OD vuông góc AB tại I
Xét ΔOIC vuông tại I và ΔOHD vuông tại H có
góc HOD chung
=>ΔOIC đồng dạng với ΔOHD
=>OI/OH=OC/OD
=>OI*OD=OH*OC