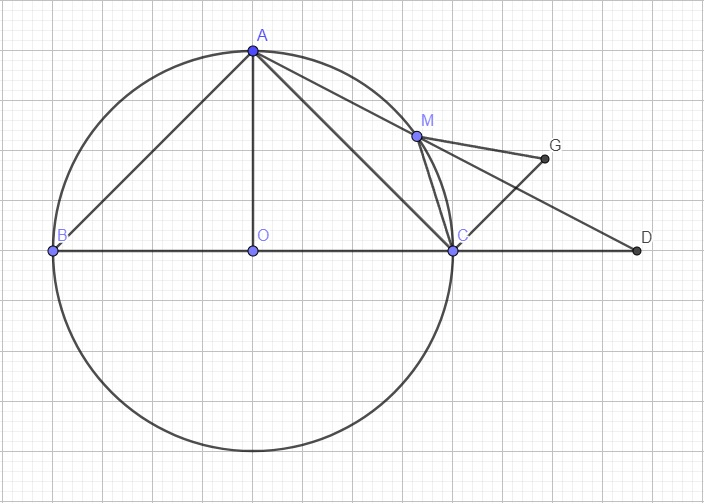
a.
Do A là điểm chính giữa cung BC \(\Rightarrow AB=AC\Rightarrow\Delta ABC\) vuông cân tại A
\(\Rightarrow AO\perp BC\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AO.BC=\dfrac{1}{2}R.2R=R^2\)
b.
Tứ giác ABCM nội tiếp (O) \(\Rightarrow\widehat{ABC}+\widehat{AMC}=180^0\) (1)
Lại có \(\widehat{ACD}+\widehat{ACB}=180^0\) (2)
Mà \(\widehat{ABC}=\widehat{ACB}\) (\(\Delta ABC\) vuông cân tại A) (3)
(1);(2);(3) \(\Rightarrow\widehat{AMC}=\widehat{ACD}\)
Xét hai tam giác AMC và ACD có:
\(\left\{{}\begin{matrix}\widehat{CAD}\text{ chung}\\\widehat{AMC}=\widehat{ACD}\end{matrix}\right.\) \(\Rightarrow\Delta AMC\sim\Delta ACD\left(g.g\right)\) (4)
\(\Rightarrow\dfrac{AM}{AC}=\dfrac{AC}{AD}\Rightarrow AM.AD=AC^2\)
Do \(\Delta ABC\) vuông cân \(\Rightarrow AC^2=\dfrac{1}{2}BC^2=2R^2\Rightarrow AM.AD=2R^2\) không đổi
Gọi G là tâm đường tròn ngoại tiếp MCD
Từ (4) \(\Rightarrow\widehat{ADC}=\widehat{MCA}\)
Mà \(\widehat{ADC}=\dfrac{1}{2}\widehat{MGC}\) (góc nội tiếp và góc ở tâm cùng chắn cung CM)
\(\Rightarrow\widehat{ACG}=\widehat{MCA}+\widehat{MCG}=\dfrac{1}{2}\widehat{MGC}+\dfrac{1}{2}\left(180^0-\widehat{MGC}\right)=90^0\)
\(\Rightarrow AC\perp GC\)
Hay tâm G của đường tròn ngoại tiếp MCD luôn nằm trên đường thẳng cố định đi qua C và vuông góc AC