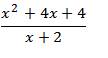Question

cho biểu thức A= x+2/x+3- 5/(x-2)(x+3)

a, Tìm điều kiện xác định và rút gọn A

b, Tính giá trị của A tại x= -2

c, Tìm x để A=5, A=0

d, Tìm x ϵ Z để A ϵ Z

Answer 1

a) ĐKXĐ: x∉{2;-3}

Ta có: \(A=\frac{x+2}{x+3}-\frac{5}{\left(x-2\right)\left(x+3\right)}\)

\(=\frac{\left(x-2\right)\left(x+2\right)}{\left(x+3\right)\left(x-2\right)}-\frac{5}{\left(x-2\right)\left(x+3\right)}\)

\(=\frac{x^2-4-5}{\left(x+3\right)\left(x-2\right)}=\frac{x^2-9}{\left(x+3\right)\left(x-2\right)}=\frac{\left(x+3\right)\left(x-3\right)}{\left(x+3\right)\left(x-2\right)}=\frac{x-3}{x-2}\)

b) Thay x=-2 vào biểu thức \(A=\frac{x-3}{x-2}\), ta được:
\(\frac{-2-3}{-2-2}=\frac{-5}{-4}=\frac{5}{4}\)

Vậy: \(\frac{5}{4}\) là giá trị của biểu thức \(A=\frac{x-3}{x-2}\) tại x=-2

c) Đặt A=5

⇒\(\frac{x-3}{x-2}=5\)

\(\Leftrightarrow x-3=5\left(x-2\right)\)

\(\Leftrightarrow x-3=5x-10\)

\(\Leftrightarrow x-3-5x+10=0\)

\(\Leftrightarrow-4x+7=0\)

\(\Leftrightarrow-4x=-7\)

hay \(x=\frac{7}{4}\)(tm)

Vậy: Khi \(x=\frac{7}{4}\) thì A=5

Đặt A=0

⇒\(\frac{x-3}{x-2}=0\)

⇔x-3=0

hay x=3(tm)

Vậy: Khi x=3 thì A=0

d) Để biểu thức A có giá trị nguyên thì x-3⋮x-2

⇔x-2-1⋮x-2

mà x-2⋮x-2

nên -1⋮x-2

⇔x-2∈Ư(-1)

⇔x-2∈{1;-1}

hay x∈{3;1}(tm)

Vậy: Khi x∈{1;3} thì A có giá trị nguyên