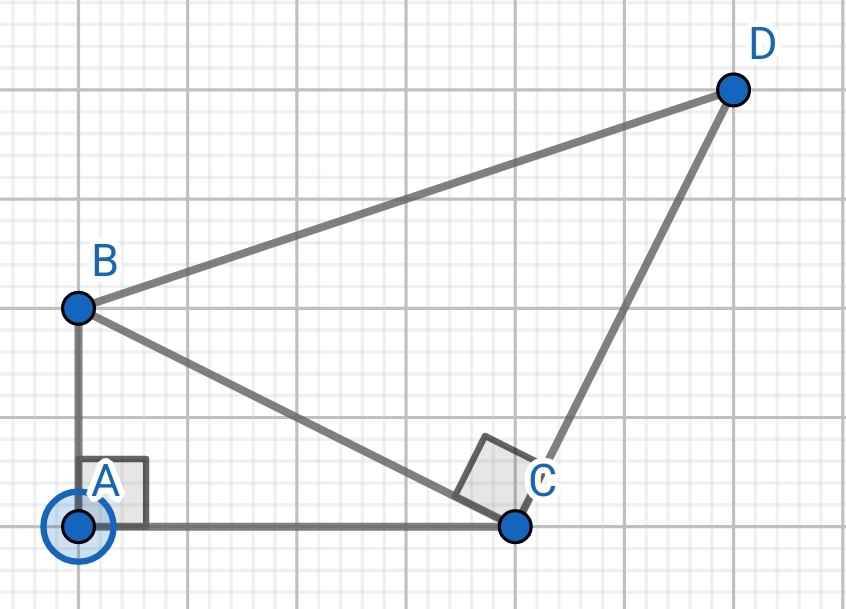
∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
⇒ AB² = BC² - AC²
= 12² - 8²
= 80
⇒ AB = \(4\sqrt{5}\) (cm)
∆CDB vuông tại C
⇒ BD² = CD² + BC² (Pytago)
⇒ CD² = BD² - BC²
= 18² - 12²
= 180
⇒ CD = \(6\sqrt{5}\) (cm)
Xét ∆ABC và ∆CDB có:
\(\dfrac{BC}{BD}=\dfrac{12}{18}=\dfrac{2}{3}\)
\(\dfrac{AB}{CD}=\dfrac{4\sqrt{5}}{6\sqrt{5}}=\dfrac{2}{3}\)
\(\dfrac{AC}{BC}=\dfrac{8}{12}=\dfrac{2}{3}\)
⇒ \(\dfrac{BC}{BD}=\dfrac{AB}{CD}=\dfrac{AC}{BC}=\dfrac{2}{3}\)
Vậy ∆ABC ∽ ∆CDB (c-c-c)













