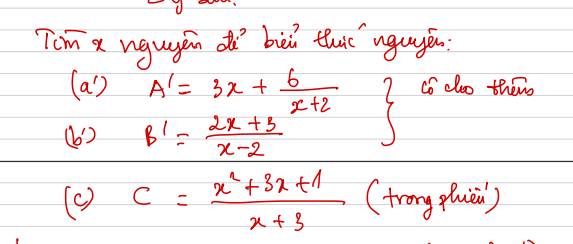Lời giải:
$C=\frac{x^2+3x+1}{x+3}=\frac{x(x+3)+1}{x+3}=x+\frac{1}{x+3}$
Với $x$ nguyên, để $C$ nguyên thì $\frac{1}{x+3}$ nguyên.
Với $x$ nguyên, để $\frac{1}{x+3}$ nguyên thì $x+3$ là ước của 1.
$\Rightarrow x+3\in \left\{1; -1\right\}$
$\Rightarrow x\in \left\{-2; -4\right\}$