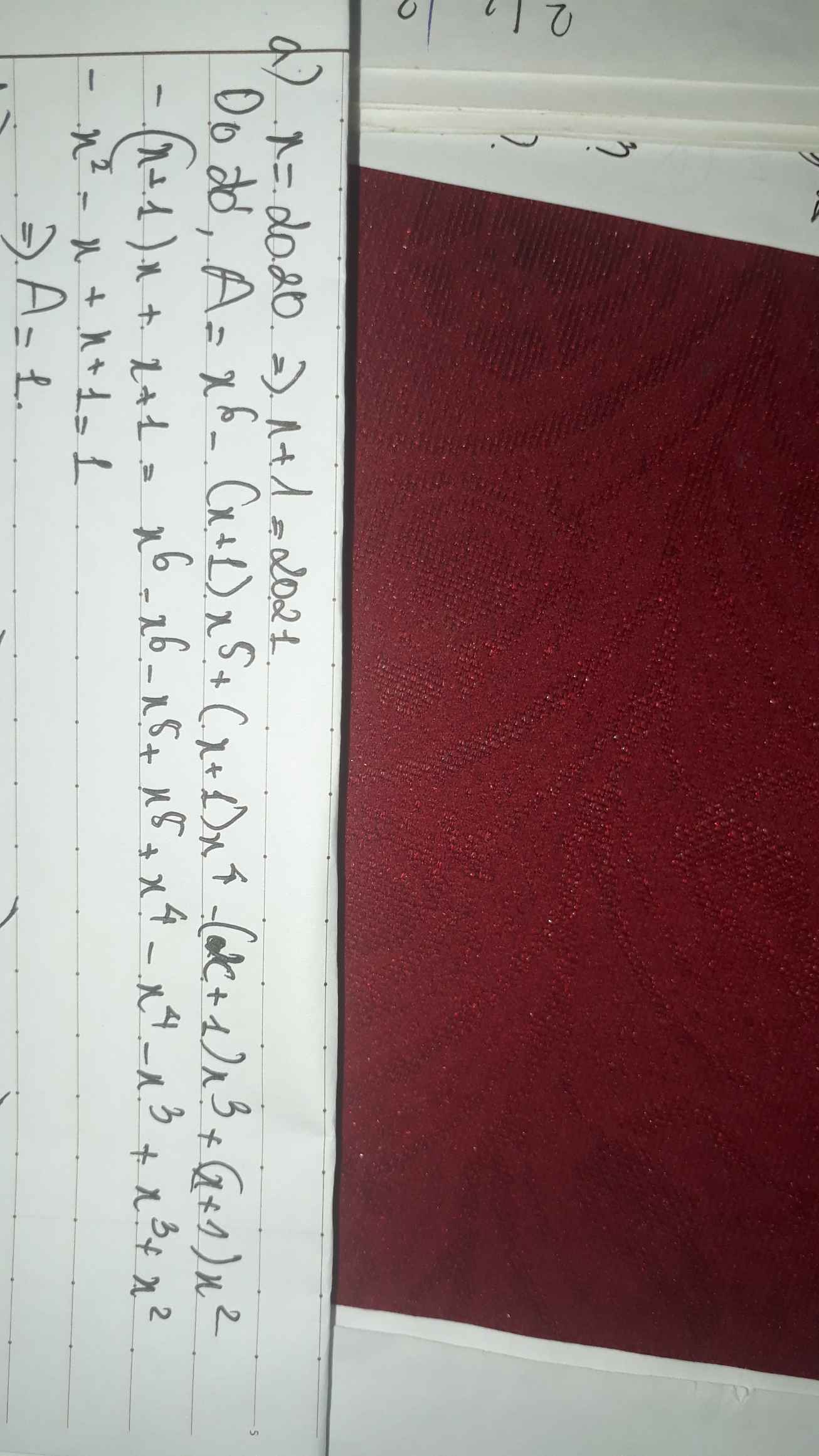a) $A= x^6-2021x^5 +2021x^4 -....+ 2021$
Có : $x=2020 \to x + 1 = 2021$
Thay vào $A$ ta có :
$A = x^6 - (x+1).x^5 + (x+1).x^4 - ....+ (x+1)$
$ = x^6 - x^6-x^5+x^5+x^4-....+x + 1$
$ = 1$
b) $B = x^{10} + 20x^9 + ...+ 20$
Ta có : $x=-19 \to x-1 = -20$ $\to 1-x = 20$.
Thay vào $B$ có :
$B = x^{10} + (1-x).x^9 + (1-x).x^8 + ...+(1-x)$
$ = x^{10} - x^{10} + x^9 - x^9 + x^8 + .... - x + 1$
$ = 1$