Bài 3:
a: ta có: AB=AD
CB=CD
Do đó: AClà đường trung trực của BD
b: Xét ΔCBA và ΔCDA có
CB=CD
BA=DA
CA chung
Do đó: ΔCBA=ΔCDA
Suy ra: \(\widehat{CBA}=\widehat{CDA}=\dfrac{360^0-180^0}{2}=90^0\)
Ai làm bài này câu 2 câu 3 hộ mình với
giúp mình bài này với!
Bài 1: Cho tứ giác ABCD có AB=AD, CB=CD, góc C =60o , góc A=100o
a, Chứng minh AC là đường trung trực của BD.
b, Tính góc B và góc D.
Bài 3: Cho tứ giác ABCD có <B +<D=180o , CB=CD. Trên tia đối của tia DA lấy điểm E, phân giác ngoài góc A và góc B cắt tại F. Chứng minh <AEB=<C+<D2<C+<D2 và <AFB=<A+<B/2
Bài 4: Cho tứ giác ABCD có <B+<D=180o , CB=CD. Trên tia đối của tia DA lấy điểm E sao cho DE=AB. Chứng minh:
a, △ABC và △EDC bằng nhau
b, AC là phân giác của góc A
Bài 5: Cho tứ giác ABCD biết số đo của các góc A,B,C,D tỉ lệ thuận với 5,8,13,10.
a, Tính số đo các góc của tứ giác ABCD.
b,Kéo dài hai cạnh AB và CD cắt nhau tại E, kéo dài hai cạnh AD và BC cắt nhau tại F. Hai tia phân giác của góc AED và góc AFB cắt nhau tại O. Phân giác góc AFB cắt cạnh CD VÀ AB lần lượt là M và N. CM: O là trung điểm đoạn MN.
giúp mình bài này với!
Bài 1: Cho tứ giác ABCD có AB=AD, CB=CD, góc C =60o , góc A=100o
a, Chứng minh AC là đường trung trực của BD.
b, Tính góc B và góc D.
Bài 3: Cho tứ giác ABCD có <B +<D=180o , CB=CD. Trên tia đối của tia DA lấy điểm E, phân giác ngoài góc A và góc B cắt tại F. Chứng minh <AEB=\(\dfrac{< C+< D}{2}\) và <AFB=<A+<B/2
Bài 4: Cho tứ giác ABCD có <B+<D=180o , CB=CD. Trên tia đối của tia DA lấy điểm E sao cho DE=AB. Chứng minh:
a, △ABC và △EDC bằng nhau
b, AC là phân giác của góc A
Bài 5: Cho tứ giác ABCD biết số đo của các góc A,B,C,D tỉ lệ thuận với 5,8,13,10.
a, Tính số đo các góc của tứ giác ABCD.
b,Kéo dài hai cạnh AB và CD cắt nhau tại E, kéo dài hai cạnh AD và BC cắt nhau tại F. Hai tia phân giác của góc AED và góc AFB cắt nhau tại O. Phân giác góc AFB cắt cạnh CD VÀ AB lần lượt là M và N. CM: O là trung điểm đoạn MN.
Bài 3: Cho hình thang cân ABCD. Đáy nhỏ AB bằng cạnh bên BC và đường chéo AC vuông góc với cạnh bên AD.
a) Tính các góc của hình thang cân.
b) Chứng minh rằng trong hình thang cân đó đáy lớn gấp đôi đáy nhỏ.
Bài 2 Cho ∆ABC cân tạiA.Gọi M là trung điểm BC. Từ điểm D thuộc BC (BD >
CD) vẽ đường vuông góc với BC cắt AC và tia BA lần lượt tại E và F.
a) Chứng minh tứ giác AMDF là hình thang vuông.
b) Gọi O là trung điểm EC, N là điểm đốixứngvới D qua O. Chứng minh tứ
giác DENC là hình chữ nhật.
c) Lấy I thuộc AB sao cho A là trung điểm IF.Chứng minh I, E, N thẳng hàng.
d) Gọi K là điểm đối xứng với N qua A.Chứng minh tứ giác BDFK là hình
chữ nhật.
Giúp mik bài 3 nhen -.-"
Ai làm bài tập 3 hộ mình với
Ai mà hộ mình bài 3 này với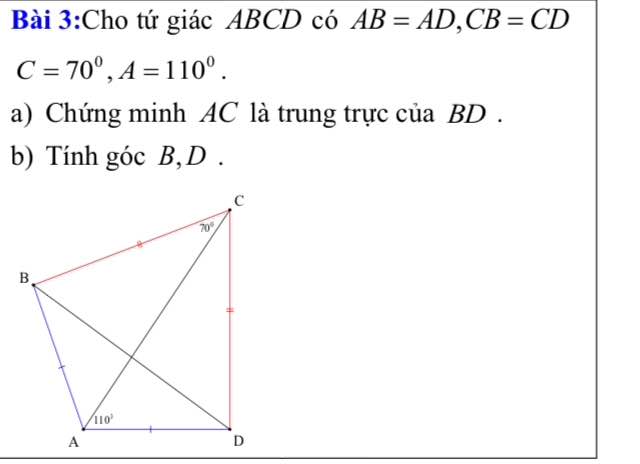
Bài 1: Tứ giác ABCD có Â =C. Chứng minh rằng các đường phân giác của góc B và góc D song song với nhau hoặc trùng nhau
Bài 2: Chứng minh rằng trong một tứ giác tổng hai đường chéo lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác.
Bài 18. Cho hình vuông ABCD, E là một điểm nằm trong hình vuông sao cho EBC [ =
ECB [ = 15o
, và F là một điểm nằm ngoài hình vuông sao cho F DC [ = F CD [ = 60o
.
Chứng minh:
1. Tam giác AED là tam giác đều.
2. Ba điểm B, E, F thẳng hàng.
