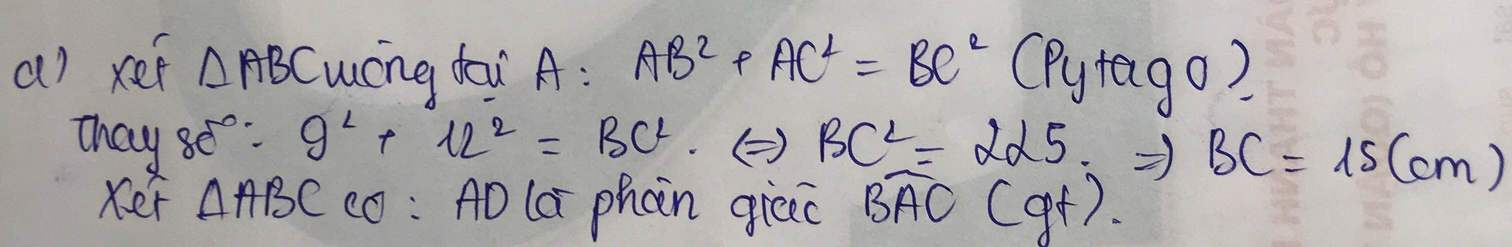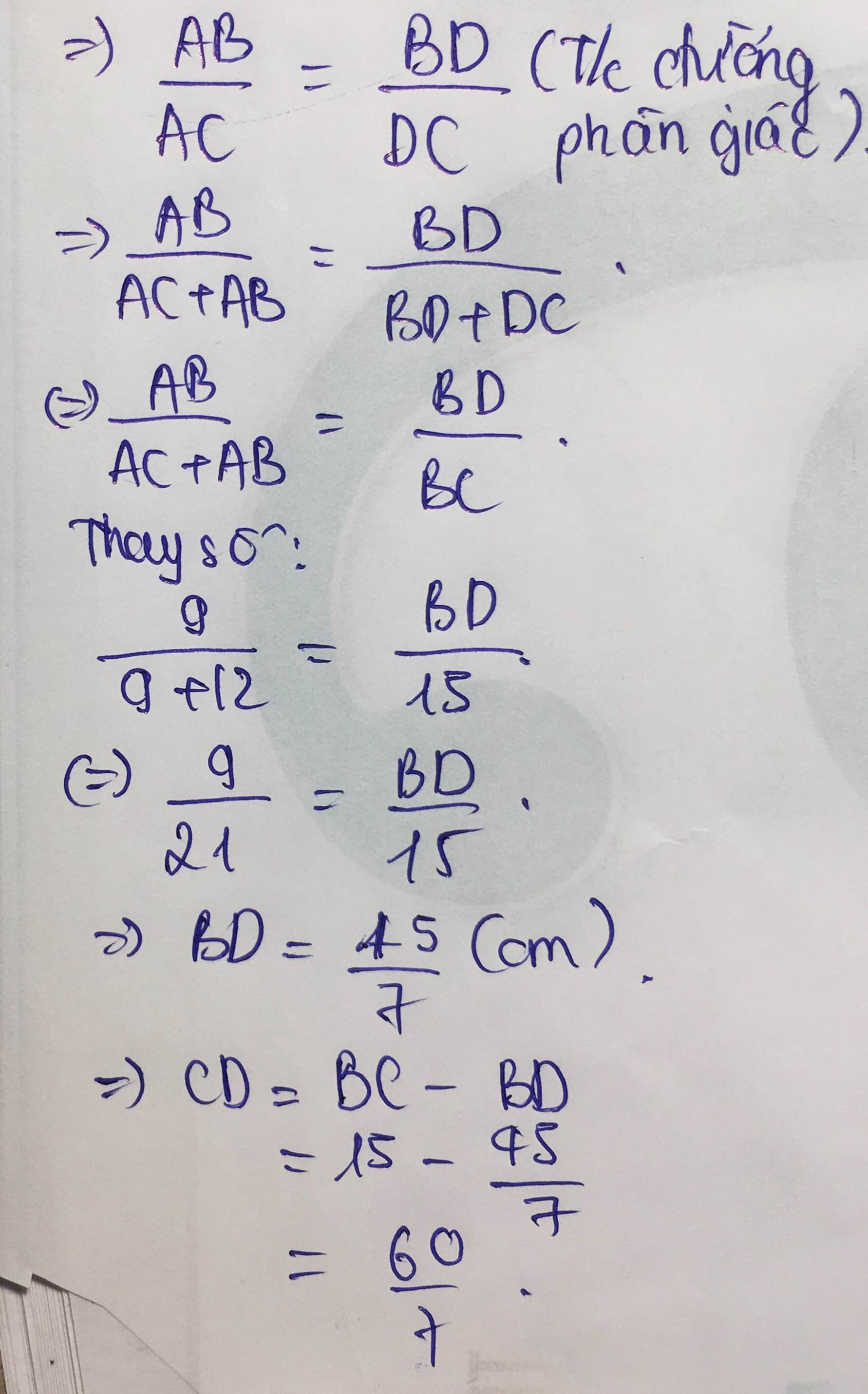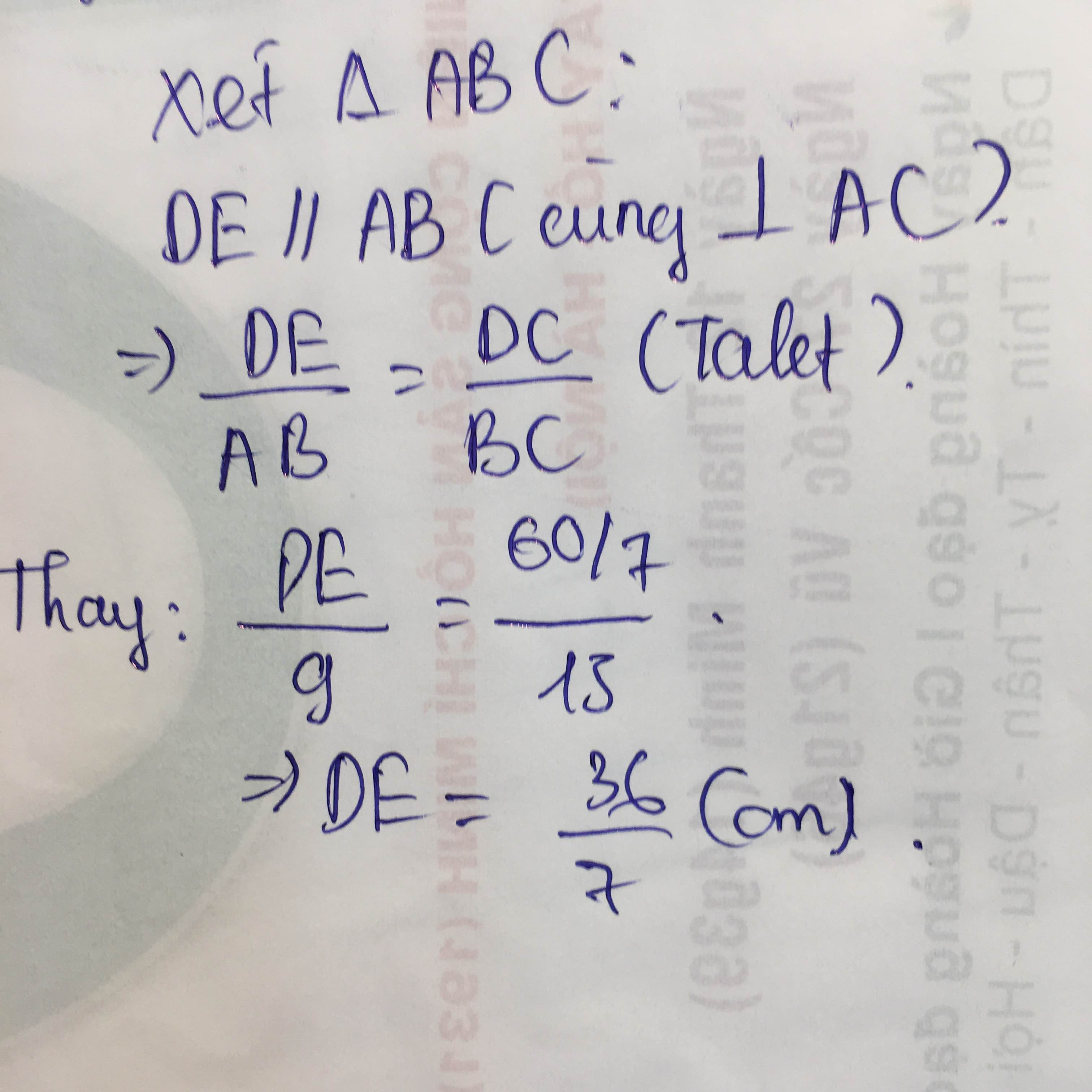Tam giác đồng dạng
Các câu hỏi tương tự
cho tam giác ABC vuông tại A , AB=12cm , AC=16cm. Vẽ đường cao AH( H thuộc BC ) và tia phân giác của góc A cắt BC tại D a/ chứng minh tam giác HBA đồng dangj tam giác ABC b/ Tính độ dài cạnh BC c/ tính tỉ số diện tích của hai tam giác ABD và ACD d/ Tính độ dài các đoạn thẳng BD và CD
Cho tam giác ABC có Â = 90°, AB = 3cm và AC = 4 cm . Đường cao AH (H thuộc BC) a, chứng minh tam giác ABC đồng dạng tam giác HAC b, chứng minh AC² = BC.HC c,Tia phân giác góc A cắt BC tại D. Tính độ dài các đoạn thẳng BC , DB
Cho tam giác ABC vuông tại A, AB < AC. AB= 3cm, AC= 4cm. Đường phân giác BD.
a, Tính BC, AD, CD
b, Qua D kẻ đường thẳng song song với AB cắt BC tại K. Chứng minh: BK.BC = AB.CK
c, Qua D kẻ đường thẳng vuông góc với BD cắt BD, AB và đường thẳng AC lần lượt tại E,G,H. Chứng minh \(\dfrac{CH}{BH}=\dfrac{KD}{AG}\)
cho tam giác abc vuông tại a có ab=3cm ac=4cm a, Chứng minh tam giác HBA đồng dạng với tam giác ABC b,Tính độ dài các đoạn thẳng BC , AH c, Gọi AD là đường phân giác của ˆ B A C ( D thuộc BC ) ; DE là đường phân giác của ˆ A D B ( E thuộc AB ) . Đường thẳng vuông góc với DE tại D , cắt cạnh AC ở F . Chứng minh rằng A E E B . D E D C . E C E A = 1
Cho tam giác ABC vuông tại A, có AB=6cm, AC=8cm và đường cao AH a. Cm tam giác ABC ~ tam giác AHB b. Tính BC,HB c. Qua B vẽ đường thẳng d vuông góc với AC, tia phân giác của góc BAC cắt BC tại M và cắt đường thẳng d tại N. Cm AB/AC= MN/AM
Cho ∆ABC vuông tại A có phân giác của góc ABC cắt AC tại D. Từ D vẽ đường thẳng song song BC cắt AB tại M. a) Giả sử AB = 6cm, AD = 3cm, CD = 5cm. Tính BC. Tính tỉ số diện tích của ∆AMD với ∆ABC b) Vẽ DE BC tại E. Chứng minh: ∆AMD ∽ ∆EDC. Từ đó suy ra: c) Từ C vẽ đường thẳng vuông góc với BD cắt BD tại I. Chứng minh: BC^2 = BD.BI + CD.CA
Cho tam giác ABC có ABAC, BE là phân giác, BD là trung tuyến (E,D thuộc cạnh AC). Đường thẳng qua C vuông góc với BE cắt BE, BD và BA lần lượt tại F, G và K. Gọi M là giao điểm của DF với BC. Chứng minh:a)M là trung điểm của đoạn thẳng BCb) DA/DE 1+BK/DFc)Đường thẳng GE song song với BCCíu với.
Đọc tiếp
Cho tam giác ABC có AB>AC, BE là phân giác, BD là trung tuyến (E,D thuộc cạnh AC). Đường thẳng qua C vuông góc với BE cắt BE, BD và BA lần lượt tại F, G và K. Gọi M là giao điểm của DF với BC. Chứng minh:
a)M là trung điểm của đoạn thẳng BC
b) DA/DE = 1+BK/DF
c)Đường thẳng GE song song với BC
Cíu với.
Cho tam giác ABC có 3 góc nhọn, đường cao BD ( D thuộc AC). Kẻ DE vuông góc với BC tại E.
a) CMR tam giác BDE đồng dạng với tam giác BCD
b) Kẻ DF vuông góc với AB tại F. CMR: BD2 = BF.BA
c) CMR góc BFE = góc BCA
d) Vẽ CG vuông góc với AB tại G. Đoạn thẳng EF cắt GD tại F. CMR H là trung điểm của GD
cho tam giác ABC vuông tại A, có đường cao AH, tia phân giác AD của góc BAC (D thuộc BC) biết AB =3cm; AC =4cm. Tính độ dài BD và DC, mong mn giúp nhé!