Question

Bài 1:

Cho tam giác ABC có góc A =90⁰;AB= 5cm;BC=10cm.Tính AC

Bài 2:

Cho tam giác ABC cân tại A.Tia phân giác của góc A cắt BC tại M.Biết AB=10cm;BC=12cm.Tính AM

Các bạn ơi giúp mình với mình cần gấp

Answer 1

Bài 1:

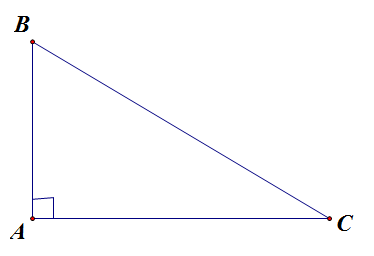
+ Xét \(\Delta ABC\) vuông tại \(A\left(gt\right)\) có:

\(AB^2+AC^2=BC^2\) (định lí Py - ta - go).

=> \(5^2+AC^2=10^2\)

=> \(AC^2=10^2-5^2\)

=> \(AC^2=100-25\)

=> \(AC^2=75\)

=> \(AC=\sqrt{75}\)

=> \(AC=5\sqrt{3}\left(cm\right)\) (vì \(AC>0\)).

Vậy \(AC=5\sqrt{3}\left(cm\right).\)

Chúc bạn học tốt!

Answer 2

Bài 1:

Áp dụng định lí Pitago trong \(\Delta ABC\) cân tại A có:

\(BC^2=AB^2+AC^2\)

\(\Rightarrow AC^2=BC^2-AB^2\)

\(\Rightarrow AC=\sqrt{10^2-5^2}=5\sqrt{3}\)

Vậy \(AC=5\sqrt{3}\)

Answer 3

1.Áp dụng Đ/L pi-ta-go ,ta có:

AB²+AC²=BC²

=>5²+AC²=10²

=>25+AC²=100

=>AC²=100-25=75

=>AC=\(\sqrt{75}\)

2.Xét \(\Delta\)AMB và \(\Delta\)AMC , có

AM (cạnh chung)

AB=AC (gt)

∠BAM=∠CAM (gt)

=>\(\Delta\)AMB=\(\Delta\)AMC (c.g.c)

=>BM=CM=\(\frac{12}{2}\)=6cm

Áp dụng Đ/L pi-ta-go , có

AM²+BM²=AB²

=>AM²+6²=10²

^=>AM²=100-36=8²

=>AM=8cm

Answer 4

Bài 2:

Ta có: \(\Delta ABC\) cân tại \(A\) và \(AM\) là tia phân giác nên:

\(\Rightarrow AM\) là đường cao và đường trung tuyến:

\(\Rightarrow BM=\frac{1}{2}BC=\frac{1}{2}.12=6cm\)

Xét \(\Delta ABM\) cân tại \(M\) có:

\(\Rightarrow AB^2=AM^2+BM^2\)

\(\Rightarrow AM^2=AB^2-BM^2\)

\(\Rightarrow AM=\sqrt{10^2-6^2}=8\)

Vậy .......

Answer 5

Áp dụng định lý Pytago vào tam giác vuông ABC ⇒BC²=AC²+AB²⇒10²=AC²+5²⇒AC²=10²-5²⇒AC²=100-25 ⇒AC²=75⇒AC=\(\sqrt{75}\)

Vậy AC=\(\sqrt{75}\)