c hình vẽ sau
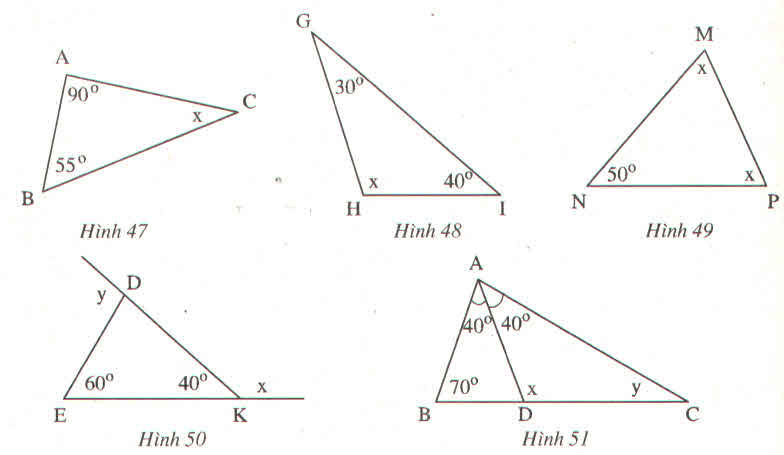
Hình a)
Ta có:\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)(tổng 3 góc 1 tam giác)
hay: \(\widehat{A}+\widehat{B}+x=180^0\)
\(\Leftrightarrow90^0+35^0+x=180\)
\(\Rightarrow x=180^0-90^0-35^0=55^0\)
Vậy x=550
b)Vì \(\widehat{HMG}+x=180^0\)(kề bù)
hay 500+x=180
\(\Rightarrow x=180^0-50^0=130^0\)
C1:
Mặc khác:\(\widehat{MHG}=180^0-\widehat{G}-\widehat{H}\)
\(\Leftrightarrow\widehat{MHG}=180^0-60^0-50^0=70^0\)
Tương tự như cách tìm x ta được :
y=\(180^0-\widehat{MHG}=180^0-70^0=110^0\)
C2 :
ta có: y=\(\widehat{G}+\widehat{H}=60^0+50^0=110^0\)(vì góc ngoài bằng tổng 2 góc trong không kề với nó)
c)Trong tam giác MNPcó:
\(\widehat{M}+\widehat{N}+\widehat{P}=180^0\)
hay x+300+200=1800
\(\Rightarrow\)x=1800-(300+200)=1300
d)Trong tam giác ABC có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
Hay\(\left(30^0+30^0\right)+70^0+y=180^0\)
\(\Rightarrow y=180^0-60^0-70^0=50^0\)
Trong tam giác AIC có:
\(\widehat{A}+\widehat{I}+\widehat{C}=180^0\)
Hay\(30^0+x+50^0=180^0\)
\(\Rightarrow x=180^0-50^0-30^0=130^0\)
e)Trong tam giác vuông 2 góc nhọn phụ nhau nên ta được:
y=900-700=300
x=900-700=300
