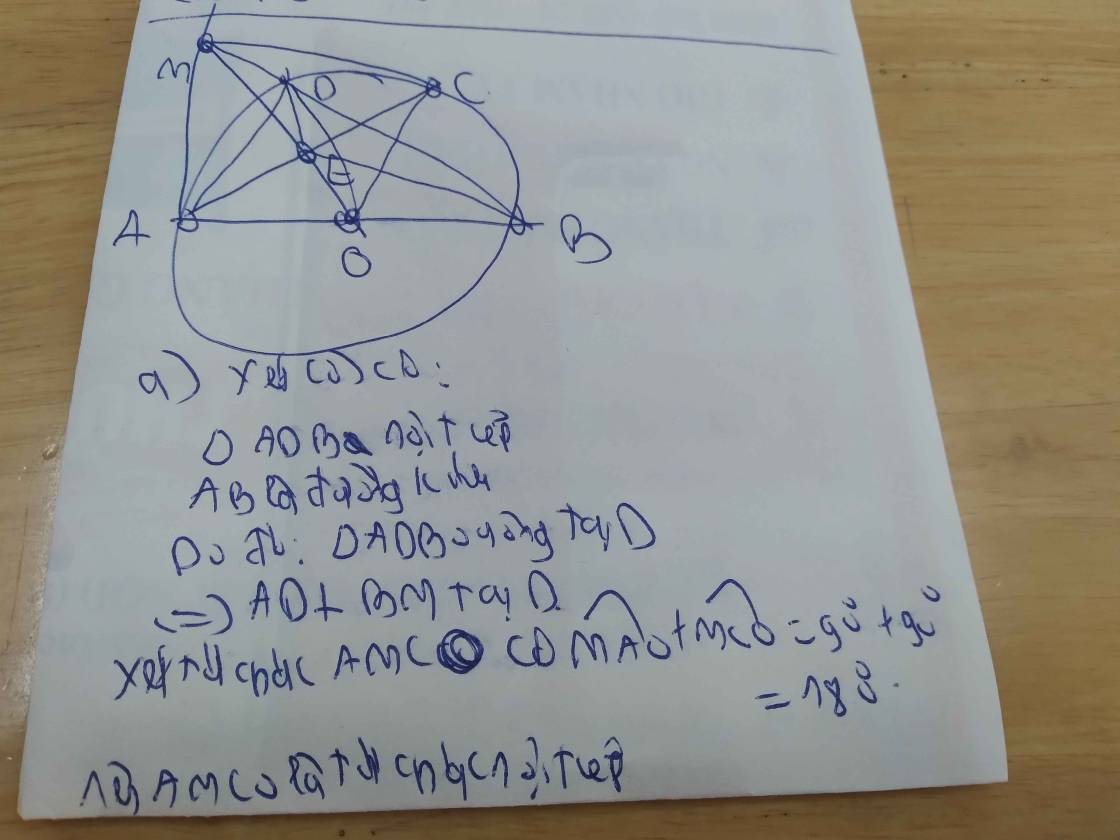
AB, kẻ cho nửa đường tròn tâm O đường kính AB. Trên nửa mặt phẳng chứa nửa đường tròn đường kính AB, kẻ Ax vuông góc với AB. Từ điểm M trên tia Ax kẻ tiếp tuyến MC ( C là tiếp điểm khác A). Đoạn thẳng AC cắt OM tại E, MB cắt nửa đường tròn tại D (D khác B). a) Chứng minh AMCO và AMDE là các tứ giác nội tiếp được đường tròn. c) Chứng minh MOD = MBE d) Gọi H là hình chiếu vuông góc của C lên AB là giao điểm của MB và CH. Chúng mình rằng El b) Chứng minh MC² = MB.MD d)
Bài 2: Đồ thị hàm số y = ax^2 (a khác 0)
Các câu hỏi tương tự
Câu 1
Cho hàm số Y= 2x + 4
A) vẽ đồ thị hàm số
B) tìm m để đường thẳng Y= 2x - 4 cắt đg thẳng Y= ( m - 1 ) x+5
Câu 2: cho đường tròn tâm O bán kính 10cm dây AB = 12cm kẻ OI vuông góc vs AB, tiếp tuyến tại A cắt OI tại M
a) tính số đo góc AOM
b) tính độ dài AM
Xem chi tiết
Chơi mà học :
Vẽ parabol
Trên một tờ giấy có kẻ dòng, chọn khoảng cách giữa hai dòng làm đơn vị độ dài, vẽ 5 đường tròn cùng tâm I có bán kính lần lượt bằng 1, 2, 3, 4, 5 (đơn vị độ dài). Đánh dấu các đường tròn này theo thứ tự là (1), (2), (3), (4), (5). Trên một tờ giấy kính, kẻ hệ trục tọa độ Oxy, trên tia Oy lấy điểm K sao cho OKdfrac{1}{2} (đơn vị độ dài nói trến). Lấy điểm Hleft(0;-dfrac{1}{2}right). Qua H kẻ đường thẳng Ht // Ox
- Đặt tờ giấy kính lên tờ giấy đã vẽ năm đường tròn sa...
Đọc tiếp
Chơi mà học :
Vẽ parabol

Trên một tờ giấy có kẻ dòng, chọn khoảng cách giữa hai dòng làm đơn vị độ dài, vẽ 5 đường tròn cùng tâm I có bán kính lần lượt bằng 1, 2, 3, 4, 5 (đơn vị độ dài). Đánh dấu các đường tròn này theo thứ tự là (1), (2), (3), (4), (5). Trên một tờ giấy kính, kẻ hệ trục tọa độ Oxy, trên tia Oy lấy điểm K sao cho \(OK=\dfrac{1}{2}\) (đơn vị độ dài nói trến). Lấy điểm \(H\left(0;-\dfrac{1}{2}\right)\). Qua H kẻ đường thẳng Ht // Ox
- Đặt tờ giấy kính lên tờ giấy đã vẽ năm đường tròn sao cho đường tròn (1) đi qua K và tiếp xúc với Ht và tâm I nằm bên phải Oy. Trên tờ giấy kính, đánh dấu vào chỗ điểm I xuất hiện và kí hiệu là điểm A
- Di chuyển tờ giấy kính sang trái sao cho đường tròn (2) đi qua K và tiếp xúc với Ht. Trên tờ giấy kính, đánh dấu vào chỗ điểm I xuất hiện và kí hiệu là điểm B (xem hình 4)
- Tiếp tục làm như thế đối với các đường tròn còn lại ta lần lượt được các điểm C, D, E trên tờ giấy kính
- Lấy các điểm A', B', C', D' , E' lần lượt đối xứng với các điểm A, B, C, D, E qua Oy
- Nối các điểm E', D', C', B', A', O, A, B, C, D, E bới một đường cong ta được một parabol
Cho parabol (P): y = \(\frac{x2}{4}\), điểm F (0:1) và đường thẳng (d): y = -1.
1) Vẽ parabol (P) và đường thẳng (d).
2) Chứng minh tất cả các điểm M trên (P) cách đều F và đường thẳng (d).
3) Một đường thẳng bất kỳ qua F cắt (P) tại 2 điểm A, B. Chứng minh rằng đường tròn đường kính AB tiếp xúc với đường thẳng (d).
Cho đường tròn O đường kính AB bằng 20 cm dây cung CD vuông góc với OA tại điểm Isao cho AI= 4 cm
a )tính Tính độ dài CI
B) Dựng các tiếp tuyến tại A và B của đường tròn Tiếp tuyến tại C cắt tiếp tuyến tại A và B lần lượt tại E và F Chứng minh EF=AF+BF
C)AC và BC cắt OE vàOFtheo thứ tự tại Mvà Ntứ giácOMCN là hình gì vì sao
Cho(O, R ) dây BC. Trên cung lớn BC lấy A (ABAC). Gọi D là điểm chính giữa cung nhỏ BC. OD cắt BC tại I. Kẻ đường thẳng qua B vuông góc với AD tại H cắt AC tại K cắt (O) tại điểm thứ 2 là E
a ) CM: BHID nội tiếp
b) EKC cân
c ) DI. DEDH. DC
d ) gọi M là giao của DE và AC .CM: khi A di chuyển trên cung lớn BC va thỏa mãn yêu cầu đề bài thì trung điểm đoạn HM luôn chuyển động trên cung tròn cố định
Đọc tiếp
Cho(O, R ) dây BC. Trên cung lớn BC lấy A (AB<AC). Gọi D là điểm chính giữa cung nhỏ BC. OD cắt BC tại I. Kẻ đường thẳng qua B vuông góc với AD tại H cắt AC tại K cắt (O) tại điểm thứ 2 là E
a ) CM: BHID nội tiếp
b) EKC cân
c ) DI. DE=DH. DC
d ) gọi M là giao của DE và AC .CM: khi A di chuyển trên cung lớn BC va thỏa mãn yêu cầu đề bài thì trung điểm đoạn HM luôn chuyển động trên cung tròn cố định
Cho(O ,R). Từ M ngoài (O) kẻ 2 tiêp tuyến MB, MA với (O) . Lấy C bất kì trên cung nhỏ AB. Gọi D, E ,F là hình chiếu của C lên AB ,AM ,BM
a )CM: AECD nội tiếp
b ) gocs CDE= CBA
c) Gọi I là giao của AC với ED, K là giao của CB với DF. CM: IK//AB
d) Xác định điểm C trên cung nhỏ AB để(AC2+CB2) min. tinh GTNNN khi OM=2R
cho ( O;R) , A∈(O) , dây BC⊥OA tại điểm M của OA
a) tứ giác OCAB là hình gì ? vì sao ?
b) kẻ tiếp tuyến với đường tròn tại B cắt OA tại E , tính BE theo R
1. cho hàm số yx2 (P) và y-2x+m (d). Tìm các giá trị của m để
a/ (d) và (P) không giao nhau
b/(d) và (P) tiếp xúc
c/(d) và (P) cắt nhau tại 2 điểm phân biệt
2. trong MPTĐ Oxy, cho (P) là đồ thị của h/s yaxx(a khác 0), bt rằng (P) đi qua điểm A(-2;-1)
a/ Gọi B là điểm thuộc (P) có hoành độ là 4. Viết pt đường thẳng AB
b/ lập phương trình đường thẳng tiếp xúc (P) và song song với đường thẳng AB
Đọc tiếp
1. cho hàm số y=x2 (P) và y=-2x+m (d). Tìm các giá trị của m để
a/ (d) và (P) không giao nhau
b/(d) và (P) tiếp xúc
c/(d) và (P) cắt nhau tại 2 điểm phân biệt
2. trong MPTĐ Oxy, cho (P) là đồ thị của h/s y=axx(a khác 0), bt rằng (P) đi qua điểm A(-2;-1)
a/ Gọi B là điểm thuộc (P) có hoành độ là 4. Viết pt đường thẳng AB
b/ lập phương trình đường thẳng tiếp xúc (P) và song song với đường thẳng AB
Bài 8: Cho (P): y-dfrac{x^2}{4} và điểm M (1;-2)1. Viết Phương trình đường thẳng (d) đi qua M và có hệ số góc là m 2. Chứng minh: (d) luôn cắt (P) tại hai điểm phân biệt A và B khi m thay đổi3. Gọi xA, yA lần lượt là hoành độ của A và B. Xác định m để left(x_Aright)^2x_B+left(x_Bright)^2x_A đạt giá trị nhỏ nhất và tính giá trị đó?
Đọc tiếp
Bài 8: Cho (P): \(y=-\dfrac{x^2}{4}\) và điểm M (1;-2)
1. Viết Phương trình đường thẳng (d) đi qua M và có hệ số góc là m 2. Chứng minh: (d) luôn cắt (P) tại hai điểm phân biệt A và B khi m thay đổi
3. Gọi xA, yA lần lượt là hoành độ của A và B. Xác định m để \(\left(x_A\right)^2x_B+\left(x_B\right)^2x_A\) đạt giá trị nhỏ nhất và tính giá trị đó?
Bài 1: Giải các pt sau:
a) x^4-5x^2+40
b) frac{150}{x}+frac{150}{x+25}5
c) 3x^2-x-40
d) frac{100}{x}-frac{100}{x+10}frac{1}{2}
Bài 2: Cho (P): yfrac{-x^2}{4}
a) Vẽ (P)
b) Tìm M in (P) sao cho M có hoành độ bằng frac{1}{3} tung độ
Bài 3: Cho pt (ẩn x): x^2-2mx+2m-20 (1)
a) Chứng minh rằng pt (1) luôn có 2 nghiệm phân biệt với mọi m
b) Tìm m để pt (1) có 2 nghiệm x_1;x_2 thỏa x^{_13}-x_2^34left(x_1^2-x_2^2right)
Bài 4: Cho DeltaABC (ABAC) có 3 góc nhọn nội tiếp (O). Các đường cao BE;...
Đọc tiếp
Bài 1: Giải các pt sau:
a) \(x^4-5x^2+4=0\)
b) \(\frac{150}{x}+\frac{150}{x+25}=5\)
c) \(3x^2-x-4=0\)
d) \(\frac{100}{x}-\frac{100}{x+10}=\frac{1}{2}\)
Bài 2: Cho (P): y=\(\frac{-x^2}{4}\)
a) Vẽ (P)
b) Tìm M \(\in\) (P) sao cho M có hoành độ bằng \(\frac{1}{3}\) tung độ
Bài 3: Cho pt (ẩn x): \(x^2-2mx+2m-2=0\) (1)
a) Chứng minh rằng pt (1) luôn có 2 nghiệm phân biệt với mọi m
b) Tìm m để pt (1) có 2 nghiệm \(x_1;x_2\) thỏa \(x^{_13}-x_2^3=4\left(x_1^2-x_2^2\right)\)
Bài 4: Cho \(\Delta\)ABC (AB<AC) có 3 góc nhọn nội tiếp (O). Các đường cao BE; CF cắt nhau tại H
a) CMR: BCEF nội tiếp và xác định tâm M của đường tròn ngoại tiếp tứ giác BCEF
b) Hai đường thẳng EF và BC cắt nhau tại S. C/m: SE.SF=SC.SB
c) Vẽ đường kính AK. Gọi I là trung điểm AH. CMR: BHCK là hình bình hành
Bài 5: a) Vẽ (P): y=\(-x^2\)
b) Tìm những điểm trên (P) có khoảng cách đến trục tung là 2
Bài 6: Cho pt (ẩn x): \(x^2-4x+m-2=0\) (1)
a) Tìm m để pt (1) có nghiệm
b) Tìm m để pt (1) có 2 nghiệm thỏa mãn \(3x_1-x_2=8\)
Bài 7: Hai giá sách trong một thư viện có tất cả 357 cuốn. Sau khi chuyển 28 cuốn sách từ giá thứ nhất sang giá thứ hai thì số cuốn sách ở giá thứ nhất bằng \(\frac{1}{2}\) số cuốn sách ở giá thứ hai. Tìm số cuốn sách ban đầu của mỗi giá
Bài 8: Cho nửa (O); bán kính R; đường kính AB. Gọi C là điểm chính giữa cung AB; M \(\in\) cung nhỏ. Kẻ CI vuông góc AM tại I; CI cắt AB tại D
a) CMR: ACIO nội tiếp. Tính góc OID
b) CMR: OI là phân giác góc COM
c) Gọi N là giao điểm AM và OC. CMR: AO.AB=AN.AM
d) Khi AM qua trung điểm K của BC. Tính \(\frac{MA}{MB};AM;BM\) theo R