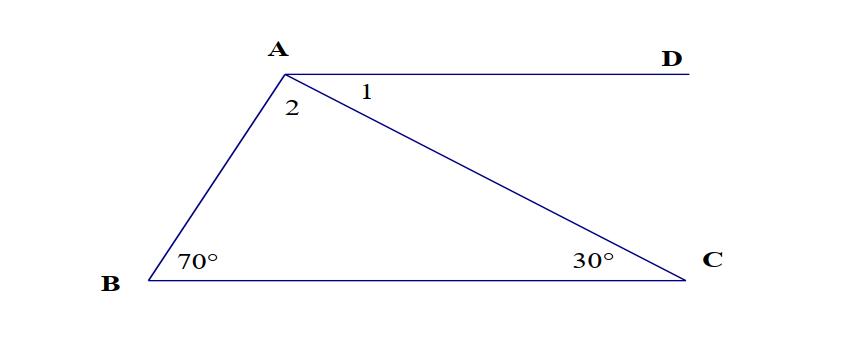
Xét \(^{\Delta}\)ABC có a//BC:
=> góc B=góc A1=30 độ( tính chất 2 đường thẳng song song)
=>góc C= góc A3=65 độ(tính chất 2 đường thẳng song song)
Ta có : góc A+góc B+góc C=180 độ (tổng 3 goc của một tam giác)
=> góc A=180-góc B-góc C=180-30-65=85 độ
Vậy góc A=85 độ
góc B=30 độ
góc C=65 độ
Giải:
Vì a // BC
Nên \(\widehat{A_1}=\widehat{C}=30^0\) (Hai góc so le trong)
Tương tự:
\(\widehat{A_3}=\widehat{B}=30^0\) (Hai góc so le trong)
\(\Rightarrow\widehat{A_2}=180^0-30^0-65^0=85^0\)
Vậy ...
Do \(\widehat{A1}\), \(\widehat{A2}\)\(\widehat{A3}\) là các góc kề bù với nhau
=> \(\widehat{A1 }\) + \(\widehat{A2}\) + \(\widehat{A3}\) =1800
\(=> góc A2 = 180^0 - A1 - A3 => A2 = 180^0 - 95^0=85^0\)
Do a // BC=> góc A3 = góc B là hai góc so le trong
mà góc A3 = \(65^0\) => góc B = \(65^0\)
Trong tam giác ABC ta có : A + B + C =1800
=> C = 1800 - A -B = 1800 - 1500
=> Góc C = 300








 A2.
A2.








