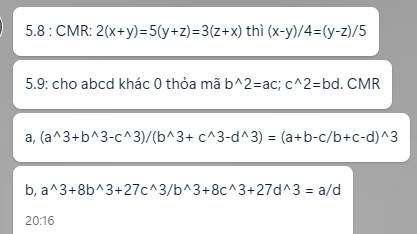Câu 5.8:
2(x+y)=5(y+z)=3(x+z)
=>\(\dfrac{x+y}{15}=\dfrac{y+z}{6}=\dfrac{x+z}{10}\)
Đặt \(\dfrac{x+y}{15}=\dfrac{y+z}{6}=\dfrac{x+z}{10}=k\)
=>\(\left\{{}\begin{matrix}x+y=15k\\y+z=6k\\x+z=10k\end{matrix}\right.\Leftrightarrow x+y+z=\dfrac{15k+6k+10k}{2}=15.5k\)
=>\(\left\{{}\begin{matrix}z=0.5k\\x=15.5k-6k=9.5k\\y=5.5k\end{matrix}\right.\)
\(\dfrac{x-y}{4}=\dfrac{9.5k-5.5k}{4}=k\)
\(\dfrac{y-z}{5}=\dfrac{5.5k-0.5k}{5}=k\)
=>\(\dfrac{x-y}{4}=\dfrac{y-z}{5}\)
Đúng 0
Bình luận (0)
