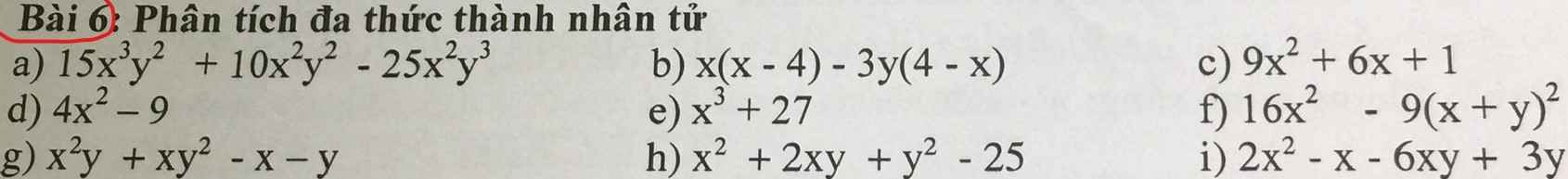2. T giải = pp giá trị riêng nhé
Gọi đa thức thương của phép chia là đa thức Q(x)
Ta có : A= 2x3 - x2 - ax - 2 = (x+1) . Q(x)
- Tại x= -1 ta có :
2.(-1)3 - (-1)2 - a.(-1) - 2 = 0
-2 -1 +a -2 = 0
-5+a = 0
a = 5
Vậy ...
\(\text{Theo bài ra ta có : }A=2x^3-x^2-ax-2\\ B=x+1\)
Áp dụng định lí \(Bê-du\) . Ta có:
\(\text{Để }A⋮B\text{ }thì\Rightarrow A_{\left(-1\right)}=0\\ \Rightarrow2\cdot\left(-1\right)^3-\left(-1\right)^2-a\cdot\left(-1\right)-2=0\\ \Rightarrow a-5=0\\ \Rightarrow a=5\)
Vậy để \(A⋮B\text{ }thì\text{ }a=5\)