Question

1.Hai điểm Avà B thuộc cùng 1 nửa mặt phẳng có bờ là đường thẳng xy.Khoảng cách từ điểm A đến xy bằng 12 cm,khoảng cách từ điểm B đến xy bằng 20 cm.Tính khoảng cách từ ttrung điểm C của AB đến xy.

2.Tính x,y trên hình 45,trong đó;AB//CD//EF//GH.

GIÚP MIK VỚI MIK CẦN GẤP LẮM Ạ !!!

Answer 1

Bài 1 : Ta có : AH , BK vuông góc với xy ( H và K là chân đường vuông góc hạ từ 2 điểm A , B xuống đường thẳng xy)

=> AH // BK

=> ABKH là hình thang

Mà CI vuông góc với xy ( I là chân đường vuông góc hạ từ điểm C xuống đường thẳng xy )

=> AH // BK // CI ( cùng vuông góc với xy ) ( 1 )

Lại có : CA = CB ( 2 )

Từ ( 1 ) và ( 2 ) suy ra IH = IK ( 3 )

Từ ( 1 ) và ( 3 ) => CI là đường trung bình của hình thang ABKH

=> CI = \(\dfrac{BK+AH}{2}\) = \(\dfrac{20+12}{2}\) = 16 ( cm )

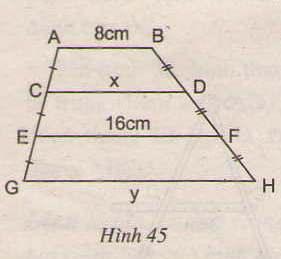
Bài 2 :

+) Xét hình thang ABFE có : AC = CE ( gt )

BD = DF ( gt )

=> CD là đường trung bình của hình thang ABFE

=> CD = x = \(\dfrac{AB+EF}{2}\)= \(\dfrac{8+16}{2}\)= 12 (cm)

+) Xét hình thang CDHG có : CE = EG ( gt )
DF = HF ( gt )

=> EF là đường trung bình của hình thang CDHG

=> EF = \(\dfrac{CD+GH}{2}\)

=> 2 EF = CD + GH

=> - GH = CD - 2EF

=> - GH = 12 - 2 . 16

=> - GH = 12 - 32

=> - GH = -20

=> GH = y = 20 ( cm )