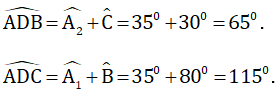1.Cho tam giác ABC vuông tại A. Tính tổng ∠B + ∠C
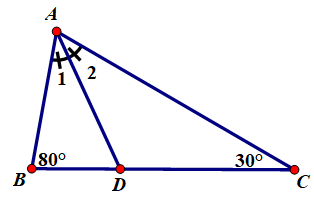
2.Cho tam giác ABC có góc B = 80 độ, góc C = 30 độ. Tia phân giác của góc A cắt BC tại D. Tính góc ADC và góc ADB
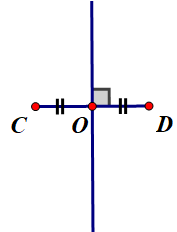
3.Cho đoạn thẳng CD dài 3cm. Hãy vẽ đường trung trực của đoạn thẳng ấy
4.Bài 2: Cho tam giác ABC có Aˆ=90o, M là trung điểm của AC. Trên tia đối của tia MB lấy điểm K sao cho MK = MB. Chứng minh rằng:
a) KC vuông góc với AC
b) AK // BC
Câu 3:
Cách vẽ
- Dùng thước có chia khoảng vẽ đoạn thẳng CD=3cm. Vẽ trung điểm O của CD bằng cách lấy O sao cho CO =1,5cm
- Dùng eke vẽ đường thẳng d vuông góc với CD tại O
- Đường thẳng d chính là đường trung trực của CD.- Dùng eke vẽ đường thẳng d vuông góc với CD tại I. Đường thẳng d chính là đường trung trực của CD
Câu 4:
a) Xét Δ AMB và Δ CMK có
AM=MC(gt)
góc AMB=góc CMK (hai góc đối đỉnh)
MB=MK(gt)
⇒ Δ AMB=Δ CMK(c.g.c)
⇒ góc MAB=góc MCK(hai góc tương ứng)
mà góc MAB=góc MCK=90o
⇒ KC⊥AC
b) Xét Δ CMB và Δ AMK có
CM=AM (gt)
góc AMK=góc CMB (hai góc đối đỉnh)
MB=MK (gt)
⇒ Δ CMB=Δ AMK (c.g.c)
⇒ góc BCM =góc MAK (hai góc tương ứng)
vì góc BCM và góc MAK là hai góc sole trong
⇒ AK//BC
Bạn tham khảo nhé!
Chúc bạn học tốt!
Câu 1:
Tổng 3 góc trong ΔABC:
∠A+∠B+∠C=180o
Mà tam giác ABC vuông tại A
=>90o+∠B+∠C=180o
=>∠B+∠C=180o-90o
=>∠B+∠C=90o
Vậy tổng 2 góc B và C bằng 90o.
Câu 2:
Áp dụng định lý góc ngoài trong các tam giác ABD và ACD ta có:
Bài 3. Cách vẽ:
- Dùng thước có chia khoảng, vẽ đoạn thẳng \(CD=3cm\). Vẽ trung điểm I của CD bằng cách lấy I sao cho \(CI=1,5cm\)
- Dùng êke vẽ đường thẳng d vuông góc với CD tại I.
Câu 1: Trong \(\Delta\)ABC có :\(\)
^A+^B+^C=180 (t/c tổng ba góc trong một \(\Delta\))
mà ^A=90 (gt)
\(\Rightarrow\)90+^B+^C=180
\(\Rightarrow\)^B+^C=180-90
\(\Rightarrow\)^B+^C=90
Vậy tổng ^B+^C=90 (độ)