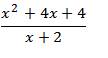Question

1)cho phân thức A=\(\frac{x^2+2x+1}{x^2-1}\)

a)với giá trị nào của x thì giá trị của phân thức được xác định

b) rút gọn A

c) tính giá trị A tại x=-2

d)tìm các giá trị nguyên của x để A có giá trị nguyên

2)cm rằng với mọi số tự nhiên n≥2 ta có \(\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{n^2}\)<\(\frac{2}{3}\)

Answer 1

a, Để giá trị của phân thức A được xác định thì \(x^2-1\ne0\)

<=> \(\left(x-1\right)\left(x+1\right)\ne0\)

=> \(\left\{{}\begin{matrix}x-1\ne0\\x+1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne1\\x\ne-1\end{matrix}\right.\)

Vậy \(x\ne0;x\ne1;x\ne-1\)

b,\(A=\frac{x^2+2x+1}{x^2-1}=\frac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}=\frac{x+1}{x-1}\)

c,Tại x=-2 thay vào A ta được : \(A=\frac{x+1}{x-1}=\frac{\left(-2\right)+1}{\left(-2\right)-1}=\frac{-1}{-3}=\frac{1}{3}\)

d, Ta có : \(A=\frac{x+1}{x-1}\) điều kiện \(x\ne0;x\ne\pm1\)

Aϵ Z => \(\frac{x+1}{x-1}\in Z\Rightarrow\frac{x-1+1+1}{x-1}\in Z\)

=> \(\frac{x-1+2}{x-1}\in Z\Rightarrow\frac{x-1}{x-1}+\frac{2}{x-1}\in Z\)

=>\(1+\frac{2}{x-1}\in Z\) mà 1 thuộc Z

nên \(\frac{2}{x-1}\in Z\)

=> \(2⋮x-1\rightarrow x-1\inƯ\left(2\right)\)

=> \(x-1\in\left\{-2;-1;1;2\right\}\)

=>\(x\in\left\{-1;0;2;3\right\}\)

theo điều kiện xác định \(x\ne0;x\ne-1\)

nên \(x\in\left\{0;2;3\right\}\)