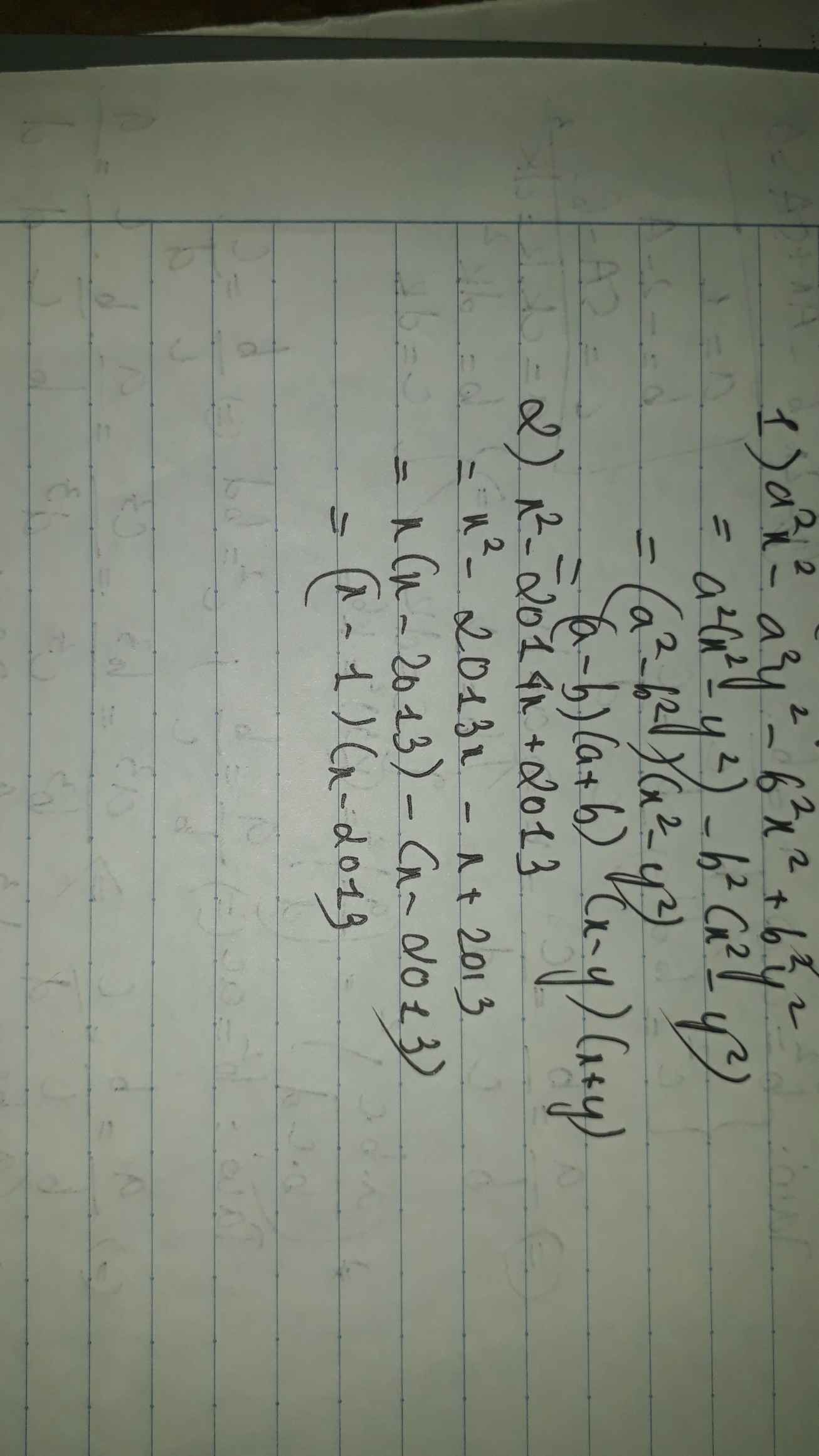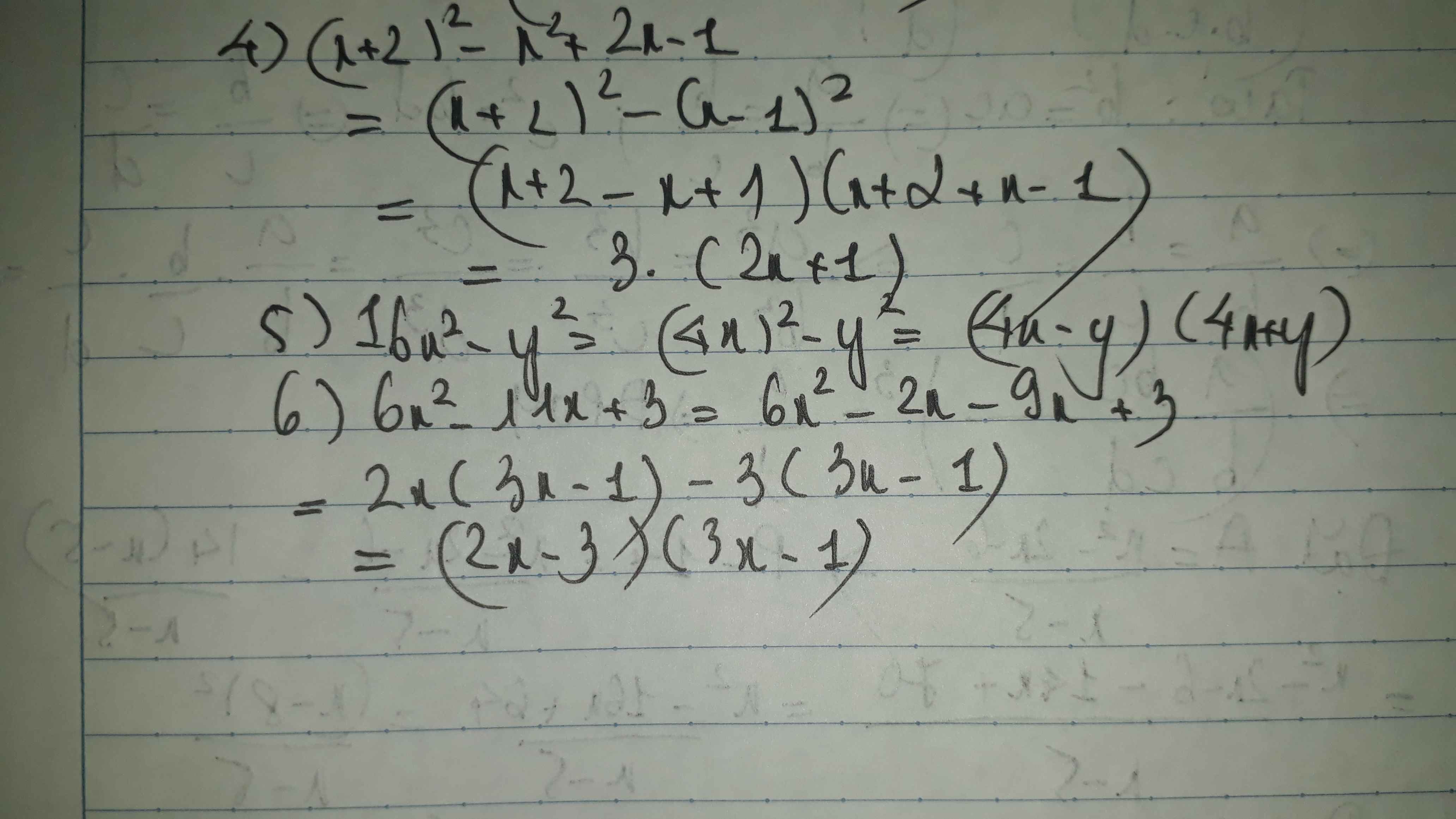1) \(a^2x^2-a^2y^2-b^2x^2+b^2y^2=a^2\left(x^2-y^2\right)-b^2\left(x^2-y^2\right)=\left(x^2-y^2\right)\left(a^2-b^2\right)=\left(x-y\right)\left(x+y\right)\left(a-b\right)\left(a+b\right)\)
2) \(x^2-2014x+2013=\left(x-1007\right)^2-1006^2=\left(x-1007-1006\right)\left(x-1007+1006\right)=\left(x-2013\right)\left(x-1\right)\)
3) \(x^2-y^2+12y-36=x^2-\left(y-6\right)^2=\left(x-y+6\right)\left(x+y-6\right)\)
4) \(\left(x+2\right)^2-x^2+2x-1=\left(x+2\right)^2-\left(x-1\right)^2=\left(x+2-x+1\right)\left(x+2+x-1\right)=3\left(2x+1\right)\)
5) \(16x^2-y^2=\left(4x-y\right)\left(4x+y\right)\)
6) \(6x^2-11x+3=6\left(x-\dfrac{11}{12}\right)^2-\dfrac{49}{24}=6\left[\left(x-\dfrac{11}{12}\right)^2-\dfrac{49}{144}\right]=6\left(x-\dfrac{11}{12}-\dfrac{7}{12}\right)\left(x-\dfrac{11}{12}+\dfrac{7}{12}\right)=6\left(x-\dfrac{3}{2}\right)\left(x-\dfrac{1}{3}\right)=\left(2x-3\right)\left(3x-1\right)\)
1: \(a^2x^2-a^2y^2-b^2x^2+b^2y^2\)
\(=a^2\left(x^2-y^2\right)-b^2\left(x^2-y^2\right)\)
\(=\left(x^2-y^2\right)\left(a^2-b^2\right)\)
\(=\left(x-y\right)\left(x+y\right)\cdot\left(a-b\right)\left(a+b\right)\)
2: \(x^2-2014x+2013=\left(x-2013\right)\left(x-1\right)\)
3: \(x^2-y^2+12y-36\)
\(=x^2-\left(y-6\right)^2\)
\(=\left(x-y+6\right)\left(x+y-6\right)\)
4: \(\left(x+2\right)^2-x^2+2x-1\)
\(=\left(x+2\right)^2-\left(x-1\right)^2\)
\(=\left(x+2-x+1\right)\left(x+2+x-1\right)\)
\(=3\left(2x+1\right)\)
5: \(16x^2-y^2=\left(4x-y\right)\left(4x+y\right)\)
6: \(6x^2-11x+3\)
\(=6x^2-9x-2x+3\)
\(=\left(2x-3\right)\left(3x-1\right)\)
3. \(x^2-y^2+12y-36\)
\(=x^2-\left(y^2-12y+36\right)\)
\(=x^2-\left(y-6\right)^2\)
\(=\left(x-y+6\right)\left(x+y-6\right)\)