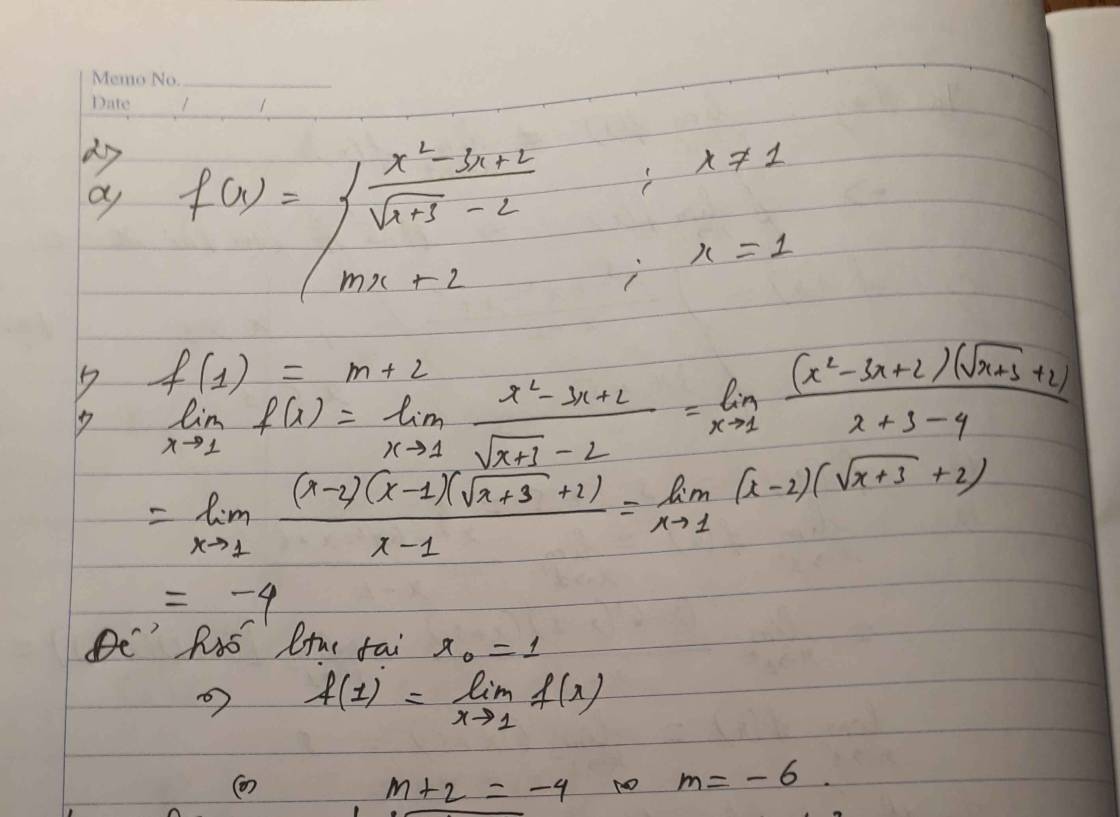1/ Xét tính liên tục của hàm số tại một điểm:
a) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{x^2-4}{x^2+x-2};x\ne2\\2x+1;x=2\end{matrix}\right.\) tại \(x_0=2\)
b) \(f\left(x\right)=\left\{{}\begin{matrix}\left(x+3\right)^3-27;x>0\\x^3+27;x\le0\end{matrix}\right.\) tại \(x_0=0\)
c) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{x^3-6x^2-x+6}{x-1};x>1\\3x+5;x\le1\end{matrix}\right.\) tại \(x_0=1\)
d) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{\sqrt{3x+10}-x-4}{x+2};x\ne-2\\-\dfrac{1}{4};x=-2\end{matrix}\right.\) tại \(x_0=-2\)
2/ Tìm \(m\) để hàm số sau liên tục tại điểm đã chỉ ra:
a) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{x^2-3x+2}{\sqrt{x+3}-2};x\ne1\\mx+2;x=1\end{matrix}\right.\) tại \(x_0=1\)
b) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{\sqrt[3]{2x^2=9}-3}{2x-6};x\ne3\\m;x=3\end{matrix}\right.\) tại \(x_0=3\)