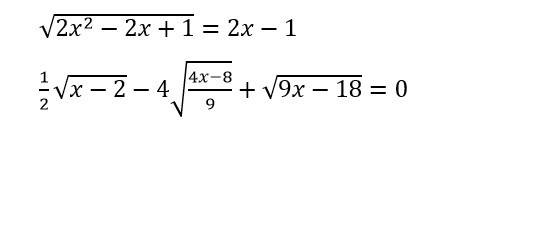a: ĐKXĐ: \(2x^2-2x+1>=0\)
=>\(x^2-x+\dfrac{1}{2}>=0\)
=>\(\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}>=0\)(luôn đúng)
Vậy: ĐKXĐ là \(x\in R\)
\(\sqrt{2x^2-2x+1}=2x-1\)
=>\(\left\{{}\begin{matrix}2x-1>=0\\4x^2-4x+1=2x^2-2x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=\dfrac{1}{2}\\2x^2-2x=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{1}{2}\\2x\left(x-1\right)=0\end{matrix}\right.\Leftrightarrow x=1\)
b: ĐKXĐ: x>=2
\(\dfrac{1}{2}\sqrt{x-2}-4\sqrt{\dfrac{4x-8}{9}}+\sqrt{9x-18}=0\)
=>\(\dfrac{1}{2}\sqrt{x-2}-4\cdot\dfrac{2}{3}\sqrt{x-2}+3\sqrt{x-2}=0\)
=>\(\sqrt{x-2}\cdot\dfrac{5}{6}=0\)
=>\(\sqrt{x-2}=0\)
=>x-2=0
=>x=2