Ta có điều kiện hiểu nhiên \(x > 0\)
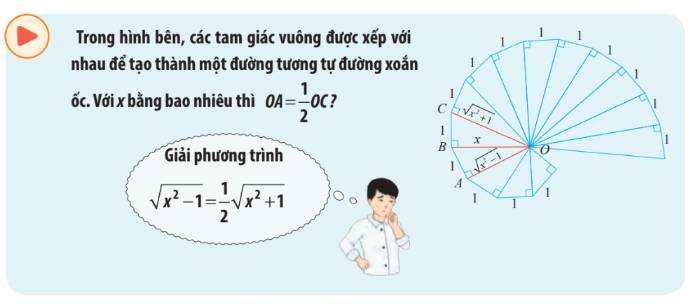
\(\begin{array}{l}\sqrt {{x^2} - 1} = \frac{1}{2}\sqrt {{x^2} + 1} \\ \Rightarrow {x^2} - 1 = \frac{1}{4}\left( {{x^2} + 1} \right)\\ \Rightarrow \frac{3}{4}{x^2} - \frac{5}{4} = 0\end{array}\)
\( \Rightarrow x = \pm \sqrt {\frac{5}{3}} \)
Thử lại, kết hợp điều kiện của x ta thấy \(x = \sqrt {\frac{5}{3}} \) thỏa mãn phương trình.
Vậy khi \(x = \sqrt {\frac{5}{3}} \) thì \(OA = \frac{1}{2}OC\)