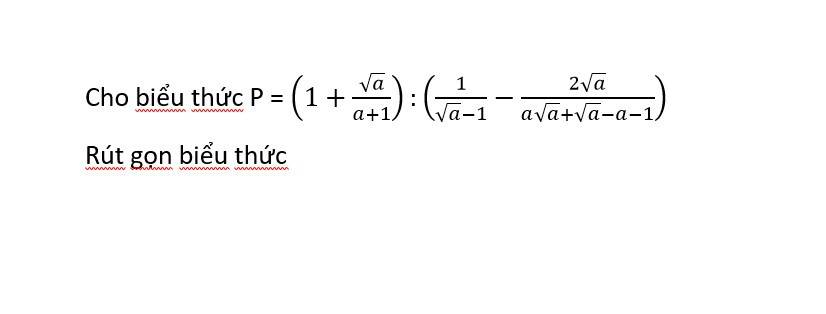\(P=\left(1+\dfrac{\sqrt{a}}{a+1}\right):\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{2\sqrt{a}}{a\sqrt{a}+\sqrt{a}-a-1}\right)\\ P=\dfrac{a+\sqrt{a}+1}{a+1}:\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{2\sqrt{a}}{a\left(\sqrt{a}-1\right)+\left(\sqrt{a}-1\right)}\right)\\ P=\dfrac{a+\sqrt{a}+1}{a+1}:\dfrac{a+1+2\sqrt{a}}{\left(\sqrt{a}-1\right)\left(a+1\right)}\\ P=\dfrac{a+\sqrt{a}+1}{a+1}:\dfrac{\left(\sqrt{a}+1\right)^2}{\left(\sqrt{a}-1\right)\left(a+1\right)}\\ P=\dfrac{a+\sqrt{a}+1}{a+1}\cdot\dfrac{\left(\sqrt{a}-1\right)\left(a+1\right)}{\left(\sqrt{a}+1\right)^2}\\ P=\dfrac{\sqrt{a^3}-1}{\left(\sqrt{a}+1\right)^2}\)
Bài 6: Biến đối đơn giản biểu thức chứa căn bậc hai
Đúng 2
Bình luận (1)
Các câu hỏi tương tự
khử mẫu của biểu thức lấy căn
\(\frac{x}{y}\) \(\sqrt{\frac{y}{x}}\) với x,y>0
2/ \(\sqrt{\frac{x}{64y^3}}\) với x,y>0
Rút gọn:a)dfrac{5sqrt{2}-2sqrt{5}}{sqrt{5}-sqrt{2}}+dfrac{6}{2-sqrt{10}}b)dfrac{6}{sqrt{5}-1}+dfrac{7}{1-sqrt{3}}-dfrac{2}{sqrt{3}-sqrt{5}}c)left(dfrac{sqrt{14}-sqrt{7}}{1-sqrt{2}}+dfrac{sqrt{15}-sqrt{5}}{1-sqrt{3}}right)divdfrac{1}{sqrt{7}-sqrt{5}}d)sqrt{2}+dfrac{1}{sqrt{5+2sqrt{6}}}+dfrac{2}{sqrt{8+2sqrt{15}}}e)left(dfrac{15}{sqrt{6}+1}+dfrac{4}{sqrt{6}-2}-dfrac{12}{3-sqrt{6}}right)timesleft(sqrt{6}+11right)Lm nhanh giúp mk nhé, mk đang cần gấp!
Đọc tiếp
Rút gọn:
a)\(\dfrac{5\sqrt{2}-2\sqrt{5}}{\sqrt{5}-\sqrt{2}}+\dfrac{6}{2-\sqrt{10}}\)
b)\(\dfrac{6}{\sqrt{5}-1}+\dfrac{7}{1-\sqrt{3}}-\dfrac{2}{\sqrt{3}-\sqrt{5}}\)
c)\(\left(\dfrac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}+\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right)\div\dfrac{1}{\sqrt{7}-\sqrt{5}}\)
d)\(\sqrt{2}+\dfrac{1}{\sqrt{5+2\sqrt{6}}}+\dfrac{2}{\sqrt{8+2\sqrt{15}}}\)
e)\(\left(\dfrac{15}{\sqrt{6}+1}+\dfrac{4}{\sqrt{6}-2}-\dfrac{12}{3-\sqrt{6}}\right)\times\left(\sqrt{6}+11\right)\)
Lm nhanh giúp mk nhé, mk đang cần gấp!
rút gọn
a.\(\dfrac{5\sqrt{2}-2\sqrt{5}}{\sqrt{5}-\sqrt{2}}+\dfrac{6}{2-\sqrt{10}}\)
b.\(\dfrac{6}{\sqrt{5}-1}+\dfrac{7}{1-\sqrt{3}}-\dfrac{2}{\sqrt{3}-\sqrt{5}}\)
lm mhanh giúp mk nhé!mk đang cần gấp!
rút gọn
a.\(\left(\dfrac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}+\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right)\div\dfrac{1}{\sqrt{7}-\sqrt{5}}\)
b.\(\sqrt{2}+\dfrac{1}{\sqrt{5+2\sqrt{6}}}+\dfrac{2}{\sqrt{8+2\sqrt{15}}}\)
Rút gọn biểu thức:
C=\(\left(\dfrac{1}{\sqrt{x}+1}-\dfrac{2\sqrt{x}-2}{x\sqrt{x}-\sqrt{x}+x-1}\right)\div\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{2}{x-1}\right)vớix\ge0,x\ne1\)
D=\(\left(\sqrt{x}+\dfrac{y-\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\right)\div\left(\dfrac{x}{\sqrt{xy}+y}+\dfrac{y}{\sqrt{xy}-x}-\dfrac{x+y}{\sqrt{xy}}\right)\)
Lm nhanh giúp mk nhé!
rút gọn
c.\(\left(\dfrac{15}{\sqrt{6}+1}+\dfrac{4}{\sqrt{6}-2}-\dfrac{12}{3-\sqrt{6}}\right)\times\left(\sqrt{6}+11\right)\)
lm nhanh giúp mk nhé
rút gọn biểu thức
a) A=\(\dfrac{\sqrt{x}-3}{\sqrt{x-2}}-\dfrac{2\sqrt{x}-1}{\sqrt{x}-1}+\dfrac{x-2}{x-3\sqrt{x}+2}vớix\ge0,x\ne4,x\ne1\)
b)\(\left(\dfrac{x+2}{x\sqrt{x}-1}-\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right)\div\dfrac{\sqrt{x}-1}{2}vớix>0,x\ne1\)