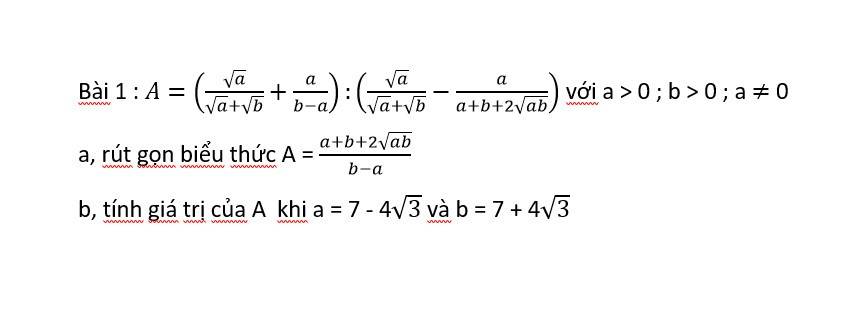a) \(A=\left(\dfrac{\sqrt[]{a}}{\sqrt[]{a}+\sqrt[]{b}}+\dfrac{a}{b-a}\right):\left(\dfrac{\sqrt[]{a}}{\sqrt[]{a}+\sqrt[]{b}}-\dfrac{a}{a+b+2\sqrt[]{ab}}\right)\left(a;b>0;a\ne\pm b\right)\)
\(\Leftrightarrow A=\left(\dfrac{\sqrt[]{a}\left(\sqrt[]{b}-\sqrt[]{a}\right)+a}{\left(\sqrt[]{a}+\sqrt[]{b}\right)\left(\sqrt[]{b}-\sqrt[]{a}\right)}\right):\left(\dfrac{\sqrt[]{a}\left(\sqrt[]{a}+\sqrt[]{b}\right)-a}{\left(\sqrt[]{a}+\sqrt[]{b}\right)^2}\right)\)
\(\Leftrightarrow A=\left(\dfrac{\sqrt[]{ab}-a+a}{\left(\sqrt[]{a}+\sqrt[]{b}\right)\left(\sqrt[]{b}-\sqrt[]{a}\right)}\right):\left(\dfrac{a+\sqrt[]{ab}-a}{\left(\sqrt[]{a}+\sqrt[]{b}\right)^2}\right)\)
\(\Leftrightarrow A=\left(\dfrac{\sqrt[]{ab}}{\left(\sqrt[]{a}+\sqrt[]{b}\right)\left(\sqrt[]{b}-\sqrt[]{a}\right)}\right):\left(\dfrac{\sqrt[]{ab}}{\left(\sqrt[]{a}+\sqrt[]{b}\right)^2}\right)\)
\(\Leftrightarrow A=\dfrac{\sqrt[]{ab}}{\left(\sqrt[]{a}+\sqrt[]{b}\right)\left(\sqrt[]{b}-\sqrt[]{a}\right)}.\dfrac{\left(\sqrt[]{a}+\sqrt[]{b}\right)^2}{\sqrt[]{ab}}\)
\(\Leftrightarrow A=\dfrac{a+b+2\sqrt[]{ab}}{b-a}\)
b) Với \(a=7-4\sqrt[]{3};b=7+4\sqrt[]{3}\)
\(\Leftrightarrow A=\dfrac{7-4\sqrt[]{3}+7+4\sqrt[]{3}+2\sqrt[]{\left(7-4\sqrt[]{3}\right)\left(7+4\sqrt[]{3}\right)}}{7+4\sqrt[]{3}-\left(7-4\sqrt[]{3}\right)}\)
\(\Leftrightarrow A=\dfrac{14+2\sqrt[]{\left[\left(7^2-\left(4\sqrt[]{3}\right)^2\right)\right]}}{7+4\sqrt[]{3}-7+4\sqrt[]{3}}\)
\(\Leftrightarrow A=\dfrac{14+2\sqrt[]{\left(49-48\right)}}{8\sqrt[]{3}}=\dfrac{16}{8\sqrt[]{3}}=\dfrac{2}{\sqrt[]{3}}=\dfrac{2\sqrt[]{3}}{3}\)