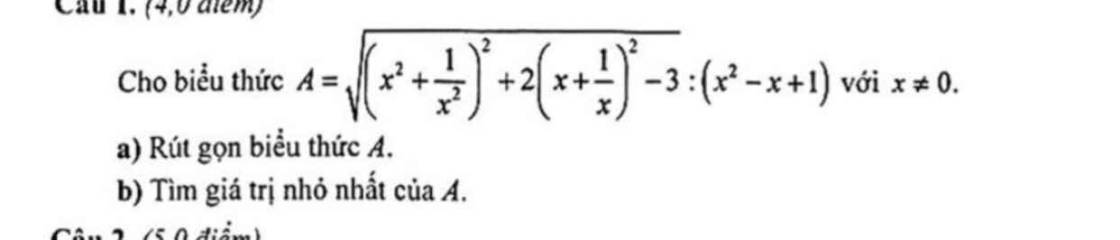(a) Ta có: \(\left(x+\dfrac{1}{x}\right)^2=x^2+\dfrac{1}{x^2}+2\)
\(\Rightarrow A=\sqrt{\left(x^2+\dfrac{1}{x^2}\right)^2+2\left(x^2+\dfrac{1}{x^2}+2\right)-3}:\left(x^2-x+1\right)\)
\(=\sqrt{\left(x^2+\dfrac{1}{x^2}\right)^2+2\left(x^2+\dfrac{1}{x^2}\right)+1}:\left(x^2-x+1\right)\)
\(=\sqrt{\left(x^2+\dfrac{1}{x^2}+1\right)^2}:\left(x^2-x+1\right)\)
\(=\left(x^2+\dfrac{1}{x^2}+1\right):\left(x^2-x+1\right)\)
\(=\dfrac{x^2+\dfrac{1}{x^2}+1}{x^2-x+1}=\dfrac{x^4+x^2+1}{x^4-x^3+x^2}\)
Vậy: \(A=\dfrac{x^4+x^2+1}{x^4-x^3+x^2}\)
(b) \(A=\dfrac{\left(x^4-x^3+x^2\right)+x^3+1}{x^4-x^3+x^2}\)
\(=1+\dfrac{x^3+1}{x^4-x^3+x^2}\)
\(=1+\dfrac{\left(x+1\right)\left(x^2-x+1\right)}{x^2\left(x^2-x+1\right)}\)
\(\Rightarrow A=1+\dfrac{x+1}{x^2}=1+\dfrac{1}{x}+\dfrac{1}{x^2}\)
\(\Rightarrow A=\left[\left(\dfrac{1}{x}\right)^2+2\cdot\dfrac{1}{x}\cdot\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2\right]-\left(\dfrac{1}{2}\right)^2+1\)
\(\Rightarrow A=\left(\dfrac{1}{x}+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
Vậy: \(MinA=\dfrac{3}{4}\Leftrightarrow x=-2\) (thỏa mãn).