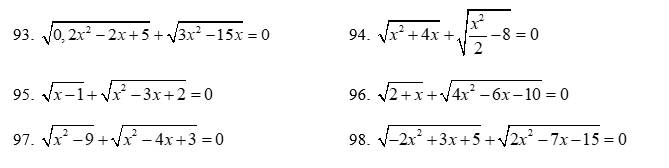\(93.\sqrt{0,2x^2-2x+5}+\sqrt{3x^2-15x}=0\\ \Leftrightarrow\sqrt{0,2x^2-2x+5}=-\sqrt{3x^2-15x}\\ ĐK:3x^2-15x\ge0\Leftrightarrow0\\ \sqrt{0,2x^2-2x+5}=-\sqrt{3x^2-15x}\\ \Leftrightarrow0,2x^2-2x+5=3x^2-15x\\ \Leftrightarrow0,2x^2-3x^2-2x+15x+5=0\\ \Leftrightarrow-2,8x^2+13x+5=0\\ \Leftrightarrow\left[{}\begin{matrix}x=5\left(tm\right)\\x=-\dfrac{5}{14}\left(ktm\right)\end{matrix}\right.\\ Vậy.S=\left\{5\right\}\)
\(94.\\ \sqrt{x^2+4x}+\sqrt{\dfrac{x^2}{2}-8}=0\\ \Leftrightarrow\sqrt{x^2+4x}=-\sqrt{\dfrac{x^2}{2}-8}\\ ĐK:x^2+4x\ge0\\ \sqrt{x^2+4x}=-\sqrt{\dfrac{x^2}{2}-8}\\ \Leftrightarrow x^2+4x=\dfrac{x^2}{2}-8\\ \Leftrightarrow\dfrac{2x^2}{2}+\dfrac{8x}{2}=\dfrac{x^2}{2}-\dfrac{16}{2}\\ \Rightarrow2x^2+8x=x^2-16\\ \Leftrightarrow2x^2-x^2+8x+16=0\\ \Leftrightarrow x^2+8x+16=0 \\ \Leftrightarrow x=-4\left(tm\right)\\ Vậy.S=\left\{-4\right\}\)
\(95.\\ \sqrt{x-1}+\sqrt{x^2-3x+2}=0 \\ \Leftrightarrow\sqrt{x-1}=-\sqrt{x^2-3x+2}\\ ĐK:x-1\ge0\Leftrightarrow x\ge1\\ \sqrt{x-1}=-\sqrt{x^2-3x+2}\\ \Leftrightarrow x-1=x^2-3x+2\\ \Leftrightarrow-x^2+3x+x-2-1=0\\ \Leftrightarrow-x^2+4x-3=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=1\left(tm\right)\end{matrix}\right.\\ Vậy.S=\left\{3;1\right\}\)
95. \(\sqrt{x-1}+\sqrt{x^2-x-2x+2}=0\)
\(\Leftrightarrow\sqrt{x-1}+\sqrt{\left(x-2\right)\left(x-1\right)}=0\)
\(\Leftrightarrow\sqrt{x-1}\left(\sqrt{x-2}+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-1}=0\\\sqrt{x-2}+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\\sqrt{x-2}=-1\left(vôlí\right)\end{matrix}\right.\)
\(\Leftrightarrow x=1\)
97. \(\Leftrightarrow\sqrt{x-3}\sqrt{x+3}+\sqrt{x-3}\sqrt{x-1}=0\)
\(\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}+\sqrt{x-1}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-3}=0\\\sqrt{x+3}=0\\\sqrt{x-1}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+3=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-3\\x=1\end{matrix}\right.\)
\(96.\\ \sqrt{2+x}+\sqrt{4x^2-6x-10}=0\\ \Leftrightarrow\sqrt{2+x}=-\sqrt{4x^2-6x-10}\\ ĐK:2+x\ge0\Leftrightarrow x\ge-2\\ \sqrt{2+x}=-\sqrt{4x^2-6x-10}\\ \Leftrightarrow2+x=4x^2-6x-10\\ \Leftrightarrow-4x^2+6x+x+10+2=0\\ \Leftrightarrow-4x^2+7x+12=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7+\sqrt{241}}{8}\left(tm\right)\\x=\dfrac{7-\sqrt{241}}{8}\left(tm\right)\end{matrix}\right.\\ Vậy.S=\left\{\dfrac{7+\sqrt{241}}{8};\dfrac{7-\sqrt{241}}{8}\right\}\)
\(97.\\ \sqrt{x^2-9}+\sqrt{x^2-4x+3}=0\\ \Leftrightarrow\sqrt{x^2-9}=-\sqrt{x^2-4x+3}\\ ĐK:x^2-9\ge0\\ \sqrt{x^2-9}=-\sqrt{x^2-4x+3}\\ \Leftrightarrow x^2-9=x^2-4x+3\\ \Leftrightarrow x^2-x^2+4x-9-3=0\\ \Leftrightarrow4x-12=0\\ \Leftrightarrow4x=12\\ \Leftrightarrow x=3\left(tm\right)\\ Vậy.S=\left\{3\right\}\)
\(98.\\ \sqrt{-2x^2+3x+5}+\sqrt{2x^2-7x-15}=0\\ \Leftrightarrow\sqrt{-2x+3x+5}=-\sqrt{2x^2-7x-15}\\ ĐK:2x^2-7x-15\ge0\\ \sqrt{-2x^2+3x+5}=-\sqrt{2x^2-7x-15}\\ \Leftrightarrow-2x^2+3x+5=2x^2-7x-15 \\ \Leftrightarrow-2x^2-2x^2+3x+7x+5+15=0\\ \Leftrightarrow-4x^2+10x+10=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5+\sqrt{65}}{4}\left(ktm\right)\\x=\dfrac{5-\sqrt{65}}{4}\left(ktm\right)\end{matrix}\right.\\ Vậy.S=\varnothing\)
93: \(\sqrt{0.2x^2-2x+5}+\sqrt{3x^2-15x}=0\)
=>0,2x^2-2x+5=0 và 3x^2-15x=0
=>3x(x-5)=0 và x^2-10x+25=0
=>3x(x-5)=0 và (x-5)^2=0
=>x-5=0
=>x=5
94: =>x^2+4x=0 và x^2/2-8=0
=>x(x+4)=0 và x^2=16
=>x=-4
95: =>x-1=0 và x^2-3x+2=0
=>x-1=0 và (x-1)(x-2)=0
=>x-1=0
=>x=1
96: =>x+2=0 và 4x^2-6x-10=0
=>x=-2
97: =>x^2-9=0 và x^2-4x+3=0
=>(x-3)(x+3)=0 và (x-3)(x-1)=0
=>x-3=0
=>x=3
98: =>-2x^2+3x+5=0 và 2x^2-7x-15=0
=>-2x^2-2x+5x+5=0 và 2x^2-10x+3x-15=0
=>(x-5)(2x+3)=0 và (x+1)(-2x+5)=0
=>\(x\in\varnothing\)