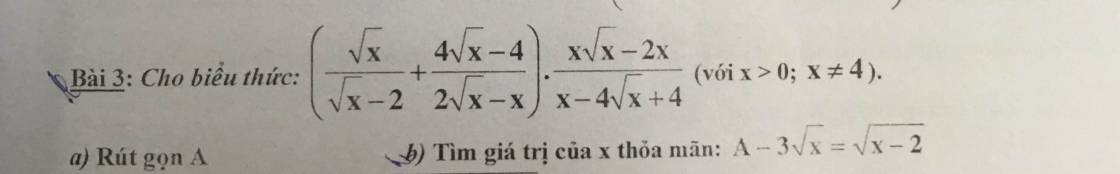a: \(A=\left(\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{4\sqrt{x}-4}{\sqrt{x}\left(\sqrt{x}-2\right)}\right)\cdot\dfrac{x}{\sqrt{x}-2}\)
\(=\dfrac{x-4\sqrt{x}+4}{\left(\sqrt{x}-2\right)^2}\cdot\dfrac{x}{\sqrt{x}}=\sqrt{x}\)
b: \(A-3\sqrt{x}=\sqrt{x-2}\)
=>x-3căn x=căn x-2
=>-2căn x=căn x-2
=>căn x-2+căn x=0
=>x-2=0 và x=0
=>\(x\in\varnothing\)
\(a,A=\left(\dfrac{\sqrt{x}}{\sqrt{x}-2}+\dfrac{4\sqrt{x}-4}{2\sqrt{x}-x}\right).\dfrac{x\sqrt{x}-2x}{x-4\sqrt{x}+4}\left(dk:x>0,x\ne4\right)\\ =\left(\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{4\sqrt{x}-4}{\sqrt{x}\left(\sqrt{x}-2\right)}\right).\dfrac{x\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)^2}\\ =\dfrac{\sqrt{x^2}-\left(4\sqrt{x}-4\right)}{\sqrt{x}\left(\sqrt{x}-2\right)}.\dfrac{x}{\sqrt{x}-2}\\ =\dfrac{x-4\sqrt{x}+4}{\left(\sqrt{x}-2\right)^2}.\sqrt{x}\\ =\dfrac{\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}-2\right)^2}.\sqrt{x}=\sqrt{x}\)
\(b,A-3\sqrt{x}=\sqrt{x-2}\Leftrightarrow\sqrt{x}-3\sqrt{x}=\sqrt{x-2}\Leftrightarrow-2\sqrt{x}=\sqrt{x-2}\left(dk:x\ge2\right)\)
\(\Leftrightarrow\left(-2\sqrt{x}\right)^2=\left(\sqrt{x-2}\right)^2\\ \Leftrightarrow4x^2=\left|x-2\right|\\ \Leftrightarrow4x^2=x-2\left(x\ge2\right)\\ \Leftrightarrow4x^2-x+2=0\)
\(\Delta=b^2-4ac=\left(-1\right)^2-4.4.2=-31< 0\)
\(\Rightarrow\) Pt vô nghiệm
Vậy không có giá trị x thỏa mãn đề bài.