\(a,\left(1-2x\right)\left(x+3\right)+\left(x+1\right)\left(2x-1\right)=14\\ \Leftrightarrow x-2x^2+3-6x+2x^2+2x-x-1=14\\ \Leftrightarrow-2x^2+2x^2+x-6x+2x-x=14+1-3\\ \Leftrightarrow-4x=12\\ \Leftrightarrow x=-3\)
\(b,\left(3x^2+x+2\right)-\left(2x+1\right)\left(2+x\right)-\left(x+4\right)\left(x-5\right)=5\\ \Leftrightarrow\left(3x^2+x+2\right)-4x-2x^2-2-x-x^2-4x+5x+20=5\\ \Leftrightarrow3x^2-2x^2-x^2+x-4x-x-4x+5x=5-20+2-2\\ \Leftrightarrow-3x=-15\\ \Leftrightarrow x=15\)
\(c,3x^2+4\left(x-1\right)\left(x+1\right)-7x\left(x-1\right)=x+12\\ \Leftrightarrow3x^2+4\left(x^2-1\right)-7x^2+7x-x=12\\ \Leftrightarrow3x^2+4x^2-7x^2+7x-x=12+4\\ \Leftrightarrow6x=16\\ \Leftrightarrow x=\dfrac{8}{3}\)
\(d,\left(2x+3\right)\left(x+4\right)+\left(x-5\right)\left(x-2\right)=\left(3x-5\right)\left(x-4\right)\\ \Leftrightarrow2x^2+3x+8x+12+x^2-5x-2x+10=3x^2-5x-12x+20\\ \Leftrightarrow2x^2+x^2-3x^2+3x+8x-5x-2x+5x+12x=-12-10+2-\\ \Leftrightarrow21x=20\\ \Leftrightarrow x=\dfrac{20}{21}\)

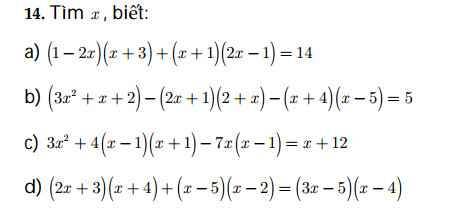








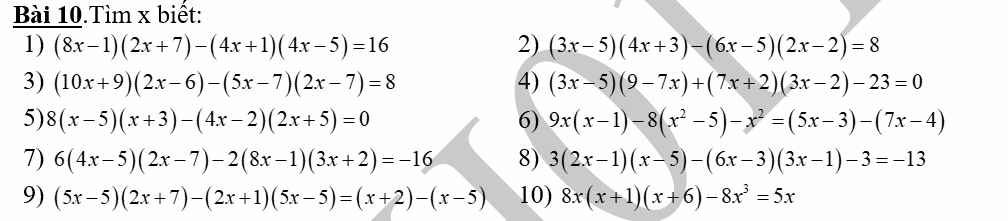 giúp em câu 6,9,10 câu này khó em k làm dc
giúp em câu 6,9,10 câu này khó em k làm dc![[Waanjai] Rùa](https://hoc24.vn/images/avt/avt29452625_256by256.jpg)
