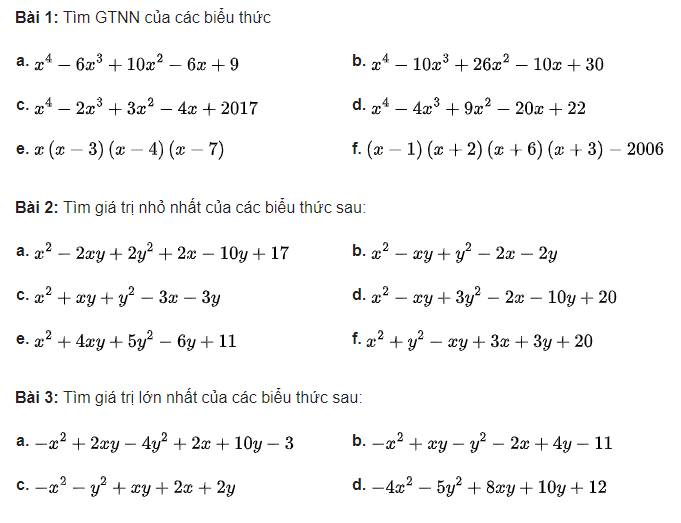Bài 3:
a: \(-x^2+2xy-4y^2+2x+10y-3\)
\(=-x^2+2xy-y^2+2x-2y-3y^2+12y-3\)
\(=-\left(x-y\right)^2+2\left(x-y\right)-1-3y^2+12y-12+10\)
\(=-\left(x-y-1\right)^2-3\left(y-2\right)^2+10\le10\forall x,y\)
Dấu '=' xảy ra khi y-2=0 và x-y-1=0
=>y=2 và x=y+1=2+1=3
b: \(-x^2+xy-y^2-2x+4y-11\)
\(=-\frac14\left\lbrack4x^2-4xy+4y^2+8x-16y+44\right\rbrack\)
\(=-\frac14\left\lbrack4x^2-4xy+y^2+8x-4y+44+3y^2-12y\right\rbrack\)
\(\) \(=-\frac14\left\lbrack\left(2x-y\right)^2+4\left(2x-y\right)+4+3y^2-12y+12+28\right\rbrack\)
\(=-\frac14\left\lbrack\left(2x-y+2\right)^2+3\left(y-2\right)^2+28\right\rbrack\le-\frac14\cdot28=-7\forall x,y\)
Dấu '=' xảy ra khi y-2=0 và 2x-y+2=0
=>y=2 và 2x=y-2=2-2=0
=>y=2 và x=0
c: \(-x^2-y^2+xy+2x+2y\)
\(=-\left(x^2+y^2-xy-2x-2y\right)\)
\(=-\frac14\left(4x^2+4y^2-4xy-8x-8y\right)\)
\(=-\frac14\left(4x^2-4xy+y^2-8x+4y+3y^2-12y\right)\)
\(=\frac{-1}{4}\left\lbrack\left(2x-y\right)^2-4\left(2x-y\right)+4+3y^2-12y+12-16\right\rbrack\)
\(=-\frac14\left\lbrack\left(2x-y-2\right)^2+3\left(y-2\right)^2-16\right\rbrack<=-\frac14\cdot\left(-16\right)=4\forall x,y\)
Dấu '=' xảy ra khi 2x-y-2=0 và y-2=0
=>y=2 và 2x=y+2=2+2=4
=>y=2 và x=2
d: \(-4x^2-5y^2+8xy+10y+12\)
\(=-4x^2+8xy-4y^2-y^2+10y-25+37\)
\(=-\left(2x-2y\right)^2-\left(y-5\right)^2+37\le37\forall x,y\)
Dấu '=' xảy ra khi 2x-2y=0 và y-5=0
=>y=5 và x=y=5
Bài 2:
a: \(x^2-2xy+2y^2+2x-10y+17\)
\(=x^2-2xy+y^2+2x-2y+y^2-8y+16+1\)
\(=\left(x-y\right)^2+2\left(x-y\right)+1+y^2-8y+16\)
\(=\left(x-y+1\right)^2+\left(y-4\right)^2\ge0\forall x,y\)
Dấu '=' xảy ra khi y-4=0 và x-y+1=0
=>y=4 và x=y-1=4-1=3
b: \(x^2-xy+y^2-2x-2y\)
\(=\frac14\left(4x^2-4xy+4y^2-8x-8y\right)\)
\(=\frac14\left(4x^2-4xy+y^2-8x+4y+3y^2-12y\right)\)
\(=\frac14\left\lbrack\left(2x-y\right)^2-4\left(2x-y\right)+4+3y^2-12y+12-16\right\rbrack\)
\(=\frac14\left\lbrack\left(2x-y-2\right)^2+3\left(y-2\right)^2-16\right\rbrack\ge\frac14\cdot\left(-16\right)=-4\forall x,y\)
Dấu '=' xảy ra khi y-2=0 và 2x-y-2=0
=>y=2 và 2x=y+2=2+2=4
=>y=2 và x=2
c: \(x^2+xy+y^2-3x-3y\)
\(=\frac14\left(4x^2+4xy+4y^2-12x-12y\right)\)
\(=\frac14\left(4x^2+4xy+y^2-12x-6y+3y^2-12y\right)\)
\(=\frac14\left\lbrack\left(2x+y\right)^2-6\left(2x+y\right)+9+3y^2-12y+12-21\right\rbrack\)
\(=\frac14\left\lbrack\left(2x+y-3\right)^2+3\left(y-2\right)^2-21\right\rbrack\ge-\frac{21}{4}\forall x,y\)
Dấu '=' xảy ra khi y-2=0 và 2x+y-3=0
=>y=2 và 2x=-y+3=-2+3=1
=>y=2 và x=0,5
d: \(x^2-xy+3y^2-2x-10y+20\)
\(=\frac14\left(4x^2-4xy+12y^2-8x-40y+80\right)\)
\(=\frac14\left\lbrack4x^2-4xy+y^2-8x+4y+11y^2-44y+80\right\rbrack\)
\(=\frac14\left\lbrack\left(2x-y\right)^2-4\left(2x-y\right)+4+11y^2-44y+44+32\right\rbrack\)
\(=\frac14\left\lbrack\left(2x-y-2\right)^2+11\left(y-2\right)^2+32\right\rbrack\ge8\forall x,y\)
Dấu '=' xảy ra khi 2x-y-2=0 và y-2=0
=>y=2 và 2x=y+2=2+2=4
=>y=2 và x=2
e: \(x^2+4xy+5y^2-6y+11\)
\(=x^2+4xy+4y^2+y^2-6y+9+2\)
\(=\left(x+2y\right)^2+\left(y-3\right)^2+2\ge2\forall x,y\)
Dấu '=' xảy ra khi y-3=0 và x+2y=0
=>y=3 và x=-2y=-6
f: \(x^2+y^2-xy+3x+3y+20\)
\(=\frac14\left(4x^2+4y^2-4xy+12x+12y+80\right)\)
\(=\frac14\left(4x^2-4xy+y^2+3y^2+12x-6y+18y+80\right)\)
\(=\frac14\left\lbrack\left(2x-y\right)^2+6\left(2x-y\right)+9+3y^2+18y+27+44\right\rbrack\)
\(=\frac14\left\lbrack\left(2x-y+3\right)^2+3\left(y+3\right)^2+44\right\rbrack\ge44\cdot\frac14=11\forall x,y\)
Dấu '=' xảy ra khi y+3=0 và 2x-y+3=0
=>y=-3 và 2x=y-3=-3-3=-6
=>y=-3 và x=-3
Bài 1:
a: \(x^4-6x^3+10x^2-6x+9\)
\(=x^4-6x^3+9x^2+x^2-6x+9\)
\(=x^2\left(x^2-6x+9\right)+\left(x^2-6x+9\right)=\left(x-3\right)^2\cdot\left(x^2+1\right)\ge0\forall x\)
Dấu '=' xảy ra khi x-3=0
=>x=3
b: \(x^4-10x^3+26x^2-10x+30\)
\(=x^4-10x^3+25x^2+x^2-10x+25+5\)
\(=x^2\left(x^2-10x+25\right)+\left(x^2-10x+25\right)+5\)
\(=\left(x^2+1\right)\left(x-5\right)^2+5\ge5\forall x\)
Dấu '=' xảy ra khi x-5=0
=>x=5
d: \(x^4-4x^3+9x^2-20x+22\)
\(=x^4-4x^3+4x^2+5x^2-20x+20+2\)
\(=x^2\left(x^2-4x+4\right)+5\left(x^2-4x+4\right)+2=\left(x-2\right)^2\cdot\left(x^2+5\right)+2\ge2\forall x\)
Dấu '=' xảy ra khi x-2=0
=>x=2
c: \(x^4-2x^3+3x^2-4x+2017\)
\(=x^4-2x^3+x^2+2x^2-4x+2+2015\)
\(=\left(x-1\right)^2\cdot\left(x^2+2\right)+2015\ge2015\forall x\)
Dấu '=' xảy ra khi x-1=0
=>x=1
e: x(x-3)(x-4)(x-7)
\(=\left(x^2-7x\right)\left(x^2-7x+12\right)\)
\(=\left(x^2-7x\right)^2+12\left(x^2-7x\right)+36-36=\left(x^2-7x+6\right)^2-36\ge-36\forall x\)
Dấu '=' xảy ra khi \(x^2-7x+6=0\)
=>(x-1)(x-6)=0
=>x=1 hoặc x=6
f: (x-1)(x+2)(x+6)(x+3)-2006
\(=\left(x^2+5x-6\right)\left(x^2+5x+6\right)-2006\)
\(=\left(x^2+5x\right)^2-36-2006=\left(x^2+5x\right)^2-2042\ge-2042\forall x\)
Dấu '=' xảy ra khi \(x^2+5x=0\)
=>x(x+5)=0
=>x=0 hoặc x=-5