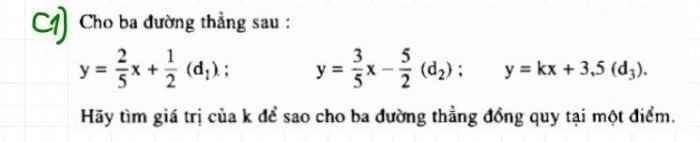Question

Answer 1

Phương trình hoành độ giao điểm của (d₁) và (d₂):

\(\dfrac{2}{5}x+\dfrac{1}{2}=\dfrac{3}{5}x-\dfrac{5}{2}\)

\(\dfrac{2}{5}x-\dfrac{3}{5}x=-\dfrac{5}{2}-\dfrac{1}{2}\)

\(-\dfrac{1}{5}x=-3\)

\(x=15\)

Thay \(x=15\) vào (d₁), ta có:

\(y=\dfrac{2}{5}.15+\dfrac{1}{2}=\dfrac{13}{2}\)

Để ba đường thẳng đồng quy thì (d₃) đi qua điểm \(\left(15;\dfrac{13}{2}\right)\)

\(\Leftrightarrow15k+3,5=\dfrac{13}{2}\)

\(\Leftrightarrow15k=\dfrac{13}{2}-\dfrac{7}{2}\)

\(\Leftrightarrow15k=3\)

\(\Leftrightarrow k=\dfrac{1}{5}\)

Vậy \(k=\dfrac{1}{5}\) thì ba đường thẳng đã cho đồng quy