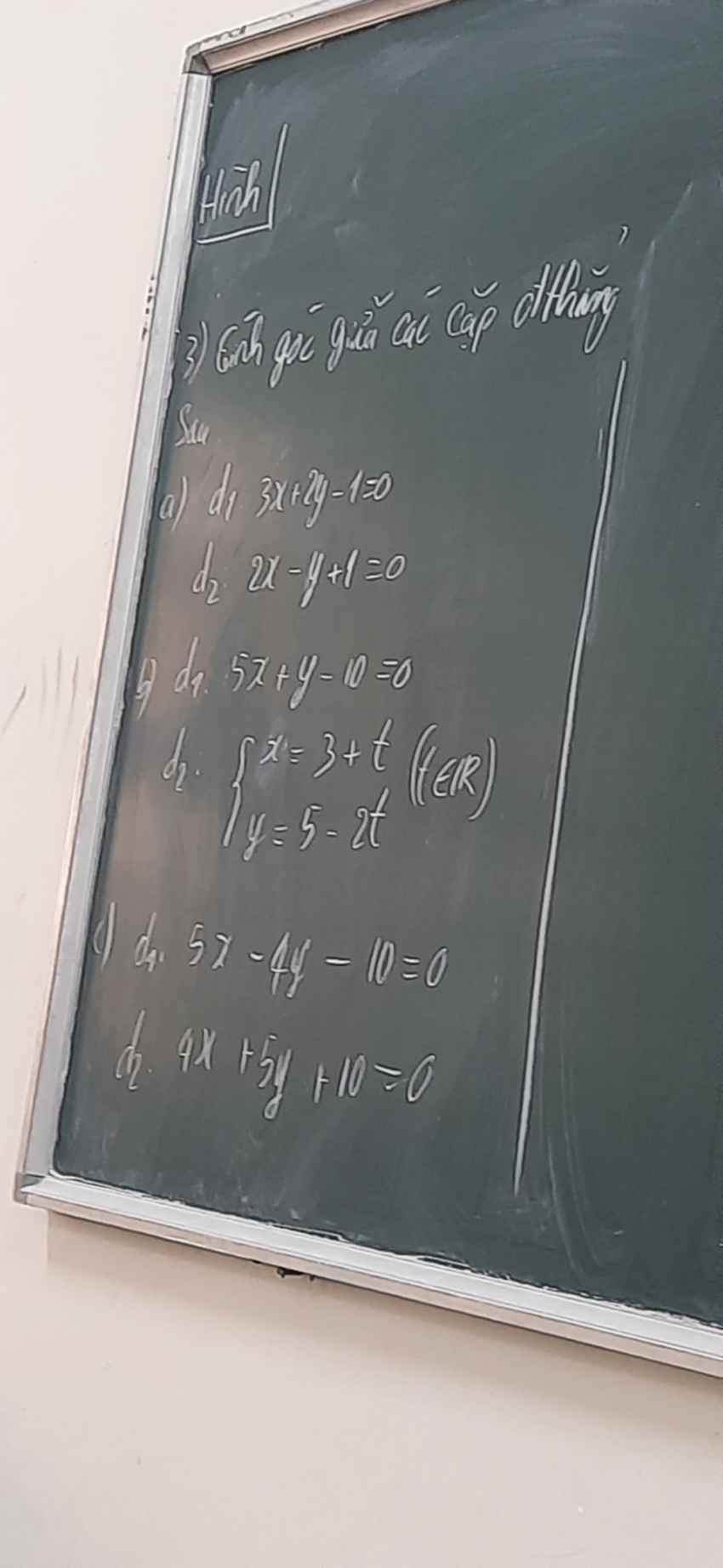a: (d1): 3x+2y-1=0
(d2): 2x-y+1=0
(d1) có vtpt là \(\overrightarrow{a}=\left(3;2\right)\)
(d2) có vtpt là \(\overrightarrow{b}=\left(2;1\right)\)
\(cos\left(d1;d2\right)=\dfrac{\left|3\cdot2+2\cdot1\right|}{\sqrt{3^2+2^2}\cdot\sqrt{2^2+1^2}}=\dfrac{8}{\sqrt{65}}\)
=>(d1;d2)=7 độ
b: (d1); vtpt là vecto a=(5;1)
(d2): x=3+t và y=5-2t
=>VTCP là (1;-2)
=>VTPT là vecto b=(2;1)
\(cos\left(d1;d2\right)=\dfrac{\left|5\cdot2+1\cdot1\right|}{\sqrt{5^2+1^2}\cdot\sqrt{2^2+1^2}}=\dfrac{11}{\sqrt{130}}\)
=>(d1;d2)=15 độ
c: (d1) có vtpt là vecto a=(5;-4)
(d2) có vtpt là vecto b=(4;5)
Vì vecto a*vecto b=0
nên (d1;d2)=90 độ
Đúng 0
Bình luận (0)
