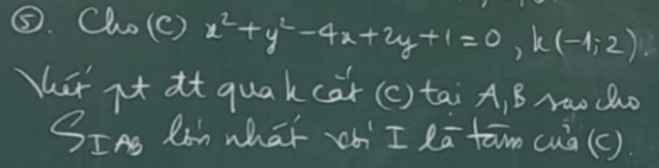Đường tròn (C) tâm \(I\left(2;-1\right)\) bán kính \(R=2\)
Ta có:
\(S_{IAB}=\dfrac{1}{2}IA.IB.sin\widehat{AIB}=\dfrac{1}{2}R^2.sin\widehat{AIB}\le\dfrac{1}{2}R^2\)
Dấu "=" xảy ra khi và chỉ khi \(sin\widehat{AIB}=1\Rightarrow\widehat{AIB}=90^0\)
\(\Rightarrow\Delta AIB\) vuông cân tại I
Gọi H là trung điểm AB \(\Rightarrow IH=d\left(I;AB\right)=\dfrac{IA}{\sqrt{2}}=\sqrt{2}\) (trung tuyến tam giác vuông cân)
Giả sử pt (d) có dạng: \(a\left(x+1\right)+b\left(y-2\right)=0\Leftrightarrow ax+by+a-2b=0\) (với \(a^2+b^2>0\))
\(d\left(I;d\right)=\dfrac{\left|2a-b+a-2b\right|}{\sqrt{a^2+b^2}}=\sqrt{2}\)
\(\Leftrightarrow\left|3a-3b\right|=\sqrt{2\left(a^2+b^2\right)}\)
\(\Leftrightarrow9a^2-18ab+9b^2=2a^2+2b^2\)
\(\Leftrightarrow7a^2-18ab+7b^2=0\)
Chọn \(a=1\Rightarrow\left[{}\begin{matrix}b=\dfrac{9+4\sqrt{2}}{7}\\b=\dfrac{9-4\sqrt{2}}{7}\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}x+1+\dfrac{9+4\sqrt{2}}{7}\left(y-2\right)=0\\x+1+\dfrac{9-4\sqrt{2}}{7}\left(y-2\right)=0\end{matrix}\right.\)
Nghiệm xấu quá