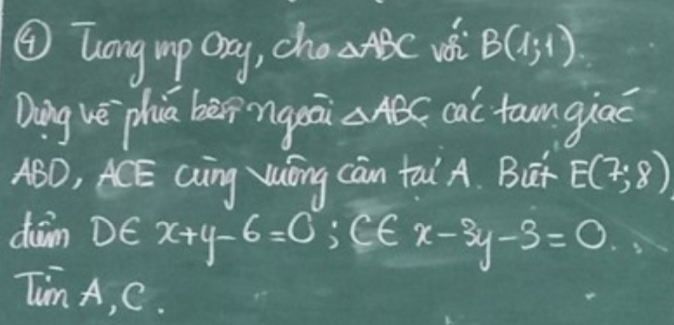Sau khi cm dc BE=DC và BE vg DC thì làm sao nữa ạ?
\(\overrightarrow{BE}=\left(6;7\right)\Rightarrow BE^2=6^2+7^2=85\)
Do D thuộc \(x+y-6=0\Rightarrow D\left(d;6-d\right)\)
C thuộc \(x-3y-3=0\Rightarrow C\left(3c+3;c\right)\)
\(\Rightarrow\overrightarrow{DC}=\left(3c+3-d;c+d-6\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{CD}.\overrightarrow{BE}=0\\CD^2=BE^2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}6\left(3c+3-d\right)+7\left(c+d-6\right)=0\\\left(3c+3-d\right)^2+\left(c+d-6\right)^2=85\end{matrix}\right.\)
Giải hệ trên (rút \(d=24-25c\) từ pt trên thế xuống dưới) ta được: \(\left[{}\begin{matrix}\left(c;d\right)=\left(1;-1\right)\\\left(c;d\right)=\left(\dfrac{1}{2};\dfrac{23}{2}\right)\end{matrix}\right.\)
\(\Rightarrow\) Tọa độ C, D
Từ đó suy ra tọa độ A (với dữ kiện 2 tam giác vuông cân)