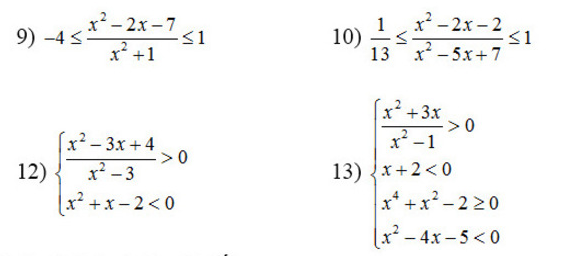1.
- Với \(m=1\) không thỏa mãn
- Với \(m\ne1\) BPT đúng với mọi x khi và chỉ khi:
\(\left\{{}\begin{matrix}m-1< 0\\\Delta=\left(2m-1\right)^2+4\left(m-1\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 1\\4m^2-3< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m< 1\\-\dfrac{\sqrt{3}}{2}< m< \dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
\(\Rightarrow-\dfrac{\sqrt{3}}{2}< m< \dfrac{\sqrt{3}}{2}\)
2.
Với \(m=\dfrac{1}{2}\) ko thỏa mãn
Với \(m\ne\dfrac{1}{2}\) BPT đúng với mọi x khi và chỉ khi:
\(\left\{{}\begin{matrix}1-2m>0\\\Delta=\left(m-2\right)^2-4\left(1-2m\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{1}{2}\\m^2+4m< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{1}{2}\\-4< m< 0\end{matrix}\right.\)
\(\Rightarrow-4< m< 0\)
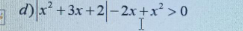Giải bpt sau :
