9.
BPT \(\Leftrightarrow -4(x^2+1)\leq x^2-2x-7\leq x^2+1\)
\(\Leftrightarrow \left\{\begin{matrix} 5x^2-2x-3\geq 0\\ 2x+8\geq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} (x-1)(5x+3)\geq 0\\ x\geq -4\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} \left[\begin{matrix} x\geq 1\\ x\leq \frac{-3}{5}\end{matrix}\right.\\ x\geq -4\end{matrix}\right.\) \(\Leftrightarrow \left\{\begin{matrix} x\geq 1\\ \frac{-3}{5}\geq x\geq -4\end{matrix}\right.\)
10
BPT $\Leftrightarrow 1\leq \frac{13x^2-26x-26}{x^2-5x+7}\leq 13$
$\Leftrightarrow x^2-5x+7\leq 13x^2-26x-26\leq 13(x^2-5x+7)$ (do $x^2-5x+7>0$ với mọi $x$)
\(\Leftrightarrow \left\{\begin{matrix} 12x^2-21x-33\geq 0\\ 39x\leq 117\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} (4x-11)(x+1)\geq 0\\ x\leq 3\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} \left[\begin{matrix} x\geq \frac{11}{4}\\ x\leq -1\end{matrix}\right.\\ x\leq 3\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} 3\geq x\geq \frac{11}{4}\\ x\leq -1\end{matrix}\right.\)
12.
BPT \(\Leftrightarrow \left\{\begin{matrix} x^2-3>0\\ (x-1)(x+2)< 0\end{matrix}\right.\) (do $x^2-3x+4>0$ với mọi $x\in\mathbb{R}$)
\(\Leftrightarrow \left\{\begin{matrix} \left[\begin{matrix} x>\sqrt{3}\\ x< -\sqrt{3}\end{matrix}\right.\\ -2< x< 1\end{matrix}\right.\)
\(\Leftrightarrow -2< x< -\sqrt{3}\)
13.
$x^2-4x-5< 0\Leftrightarrow (x+1)(x-5)< 0$
$\Leftrightarrow -1< x< 5$
$\Rightarrow x>-1\Rightarrow x>-2\Leftrightarrow x+2>0$ (mâu thuẫn với đề)
Vậy bpt vô nghiệm.

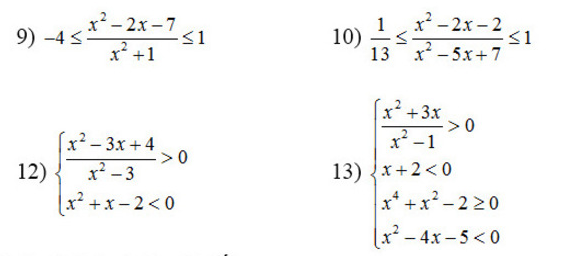





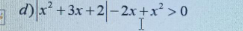 Giải bpt sau :
Giải bpt sau :



